Ряди динаміки у статистиці, види, аналітичне вирівнювання, показтели аналізу рядів динаміки, відношення рівнів, середні характеристики, приклади розвязання задач

Статистика займається не тільки обробкою накопичених даних, але і знаходженням тенденцій в різних парних показниках, які пов’язані один з одним, що успішно вирішується застосуванням інструменту «ряди динаміки в статистиці».

Класичним прикладом є зміна будь-яких показників за певний проміжок часу, що врешті-решт зводиться не до вивчення попарної залежності (показник — час), а до вивчення змін показників у динаміці.

Поняття про ряди динаміки

Суворе поняття для ряду динаміки позначено в статистиці так.

Динамічні ряди (іншими словами ряд динаміки або часовий ряд) – це розподілені в зростаючому порядку дискретних значень вибраного статистичного параметра за послідовні часові проміжки.

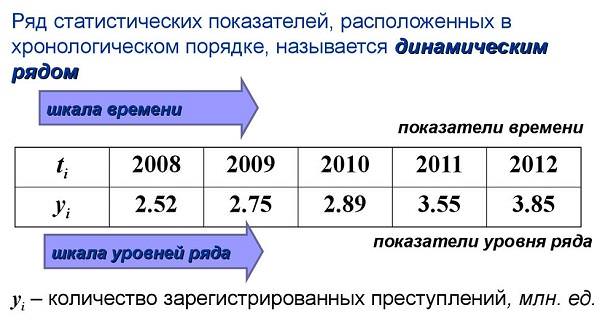
Дивіться також:  Собівартість продукції це простими словами, види, калькуляція собівартості реалізованої продукції на виробництві, приклад та аналіз розрахунку фактичної, цехової, комерційної собівартості

Якщо розглянути динамічний ряд, буде очевидно, що він наповнений даними у форматі y1t1, y2t2, y3t3…yntn. Стосовно до тимчасового ряду, значенням у називатиметься «рівень ряду», при цьому перший член ряду (у1) називається базисним (початковим) рівнем, а уп – кінцевим рівнем. Через позначення t буде позначатися часовий показник, який відповідає кожному з рівнів ряду.

При побудові графічної залежності тимчасового ряду, функція буде мати вигляд t(y), де y (ординат) будуть відкладені значення рівнів ряду (параметр), а по осі абсцис (вісь абсцис) будуть відкладені тимчасові значення параметра t.

Сторінка: 1 2 3 4 5 6 7 8