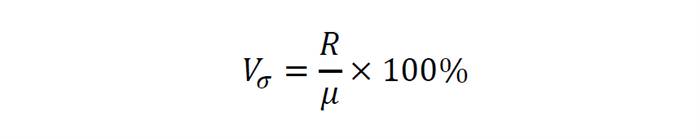Як довести, що закономірність, отримана при вивченні експериментальних даних, не є результатом збігу або помилки експериментатора, що вона достовірна? З таким питанням стикаються початківці дослідники.Описова статистика надає інструменти для вирішення цих завдань. Вона має два великих розділи – опис даних та їх зіставлення в групах або в ряду між собою.

Показники описової статистики

Існує кілька показників, які використовує описова статистика.

Середнє арифметичне

Отже, уявімо, що перед нами стоїть завдання описати зростання всіх студентів в групі з десяти осіб. Озброївшись лінійкою і провівши вимірювання, ми отримуємо маленький ряд з десяти чисел (зростання в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Якщо уважно подивитися на цей лінійний ряд, то можна виявити кілька закономірностей:

• Ширина інтервалу, куди потрапляє зростання всіх студентів, – 18 див.
• У розподілі зростання найбільш близький до середині цього інтервалу.
• Зустрічаються і винятки, які найбільш близько розташовані до верхньої або нижньої межі інтервалу.

Цілком очевидно, що для виконання завдання за описом зростання студентів у групі немає необхідності приводити всі значення, які будуть вимірюватися. Для цієї мети достатньо навести лише два, які в статистиці називаються параметрами розподілу. Це середньоарифметичне і стандартне відхилення від середнього арифметичного. Якщо звернутися до зростання студентів, то формула буде виглядати наступним чином:

Середньоарифметичне значення зростання студентів = (Сума всіх значень зростання студентів) / (Кількість студентів, які брали участь у вимірі)

Якщо звести все до строгих математичних термінах, то визначення середнього арифметичного (позначається грецькою буквою – μ (мю)) буде звучати так:

Середнє арифметичне – це відношення суми всіх значень однієї ознаки для всіх членів сукупності (X) до числа всіх членів сукупності (N).

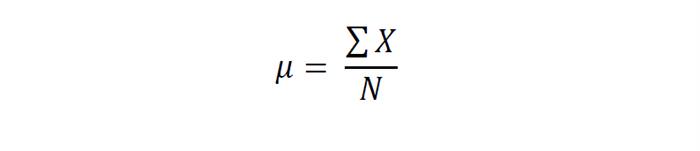
Якщо застосувати цю формулу до наших вимірів, то отримуємо, що μ для зростання студентів у групі 175,5 див.

Стандартне відхилення

Якщо придивитися до зростання студентів, який ми виміряли у попередньому прикладі, то зрозуміло, що зростання кожного на скільки-то відрізняється від обчисленого середнього (175,5 см). Для повноти опису потрібно зрозуміти, якою є різниця між середнім зростанням кожного студента і середнім значенням.

На першому етапі обчислимо параметр дисперсії. Дисперсія в статистиці (позначається σ2 (сигма в квадраті) – це відношення суми квадратів різниці середнього арифметичного (μ) і значення члена ряду (Х) до числа всіх членів сукупності (N). У вигляді формули це розраховується зрозуміліше:

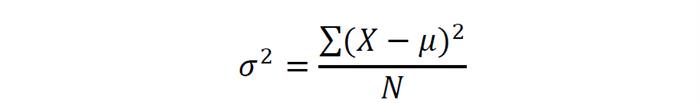
Значення, які ми отримаємо в результаті обчислення за цією формулою, ми будемо представляти у вигляді квадрата величини (в нашому випадку – квадратні сантиметри). Характеризувати зростання в сантиметрах квадратними сантиметрами, погодьтеся, безглуздо. Тому ми можемо виправити, точніше, спростити вираз і отримаємо середньоквадратичне відхилення формулу і розрахунок, приклад:

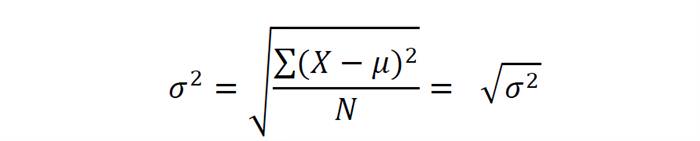
Таким чином, ми отримали величину стандартного відхилення (або середнього квадратичного відхилення) – квадратний корінь з дисперсії. З одиницями вимірювання теж тепер все в порядку, можемо порахувати стандартне відхилення для групи:

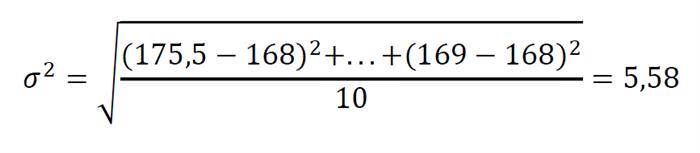
Виходить, що наша група студентів обчислюється по зростанню таким чином: 175,50±5,25 див.

Коефіцієнт варіації

Середнє квадратичне відхилення добре працює з рядами, в яких розкид значень не дуже великий (це добре видно на прикладі росту, де інтервал був всього 18 см). Якщо б ряд наших вимірів був значнішим, а варіювання зростання було сильніше, то стандартне відхилення стало непоказовим і нам знадобився би критерій, який може відобразити розкид у відносних одиницях (тобто у відсотках, відносно середньої величини).

Для цих цілей передбачені абсолютні та відносні показники варіації в статистиці, що характеризують варіаційні масштаби:

• Квадратичний коефіцієнт варіації.
• Розмах варіації.
• Коефіцієнт осциляції.

Квадратичний коефіцієнт варіації (позначається як Vσ) – це відношення середньоквадратичного відхилення до середньоарифметичному значенню, виражене у відсотках.

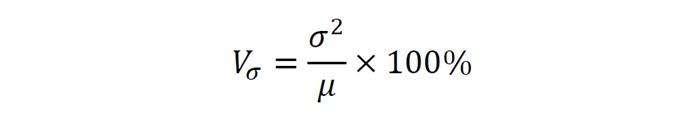
Для нашого прикладу зі студентами, визначити Vσ нескладно — він буде дорівнює 3,18%. Основна закономірність – чим більше буде змінюватися значення коефіцієнта, тим більше розкид навколо середнього значення і тим менш однорідна вибірка.

Перевага коефіцієнта варіації в тому, що він показує однорідність значень (асиметрія) в ряду наших вимірювань, крім того, на нього не впливають масштаб і одиниці вимірювання. Ці фактори роблять коефіцієнт варіації особливо популярним в біомедичних дослідженнях. Вважатиметься, що ексцес значення Vσ =33% відокремлює однорідні вибірки від неоднорідних.

Якщо знайти в ряді значень зростання (перший приклад) максимальне і мінімальне значення, то отримаємо розмах варіації (позначається як R, іноді ще називається колеблемостью). У нашому прикладі це значення буде дорівнює 18 див. Ця характеристика використовується для розрахунку коефіцієнта осциляції:

Коефіцієнт осциляції – показує як розмах варіації буде ставитися до середнього арифметичного ряду в процентному відношенні.