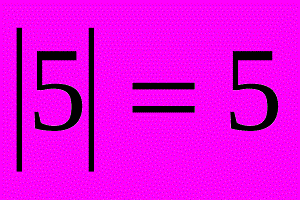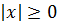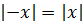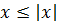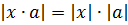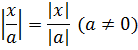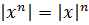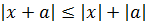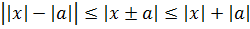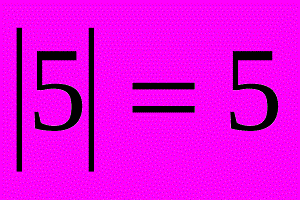
Модуль числа, рішення нерівностей з модулем, властивості, як розкрити, чому дорівнює модуль відємного числа, як вирішувати рівняння з модулем, приклади графіків

Модуль числа легко знайти, і теорії, яка лежить в його основі, важлива при вирішенні завдань.

Властивості та правила розкриття, використовувані при рішенні вправ і на іспитах, будуть корисні школярам і студентам.

Що таке модуль математики

Модуль числа описує відстань на числової лінії від нуля до точки без урахування того, у якому напрямку від нуля лежить точка. Математичне позначення: |x|.

Іншими словами, це абсолютна величина числа. Визначення доводить, що значення ніколи не буває негативним.

Дивіться також:  Вертикально: це – вгору або вниз і як виглядає вертикальна лінія

Властивості модуля

Важливо пам’ятати про наступні властивості:

  1. Правило розкриття: абсолютна величина будь-якого числа більше або дорівнює нулю:

  2. Якщо абсолютні значення містять вираження протилежних значень, вони рівні:

  3. Значення числа не перевищує величину його модуля:

  4. Правило розкриття при творі:

  5. Правило, застосовне при розподілі:

  6. При зведенні в ступінь:

  7. Сума величин:

  8. Подвійний модуль:

Сторінка: 1 2 3 4 5 6