Цей термін веде своє походження від латинського слова «varito». Воно перекладається як «зміна» або «відмінність».

Варіація — це кількісна міра зміни певних даних, яка допомагає досліджувати її випадкові зміни. Для їх аналізу застосовують різні статистичні методи.

Про них буде більш докладно розказано в цій статті.

Показники варіації в статистиці

Статистика широко застосовується в самих різних областях. Вона довела свою користь не тільки в природничих науках, але й у вивченні різних соціологічних явищ, змін цін, а також в інших ситуаціях.

Ця наука має справу з випадковими величинами, зміна яких вимагає для свого опису використання спеціальних характеристик. Найбільш відомою з них є середня. Однак, хоча вона й включає в себе певний обсяг інформації, тим не менш не дає можливості знайти інформацію про розкид випадкових даних, а також дати поняття про динаміку зміни і найбільш ймовірні тенденції в подальшому.

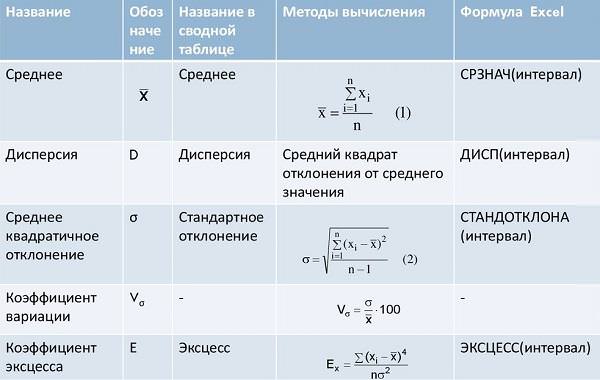
Математичний апарат для вивчення варіаційних процесів використовує характеристики, способи розрахунку яких можна розділити на три групи.

В їх число входять:

1. Показники розмаху.
2. Цифри, що дають поняття про величину відхилення.
3. Відносні показники, які відносяться до варіації.

Показники розмаху змін говорять про те, яка різниця між максимальними відхиленнями досліджуваних чисел:

• варіаційний розмах;
• децильный розмах;
• квартильный розмах.

Дані, що відносяться до другої категорії, можна вважати так:

• середнє лінійне відхилення;
• середнє квадратичне;
• дисперсія.

Для розрахунку відносних показників застосовується:

• відносний квартильный розмах;
• лінійний коефіцієнт;
• коефіцієнт варіації.

Далі буде розказано про найбільш часто застосовуваних математичних характеристики розглянутого поняття.

При проведенні статистичних обчисленнях зручно користуватися електронними таблицями Excel.