Канонічне рівняння параболи

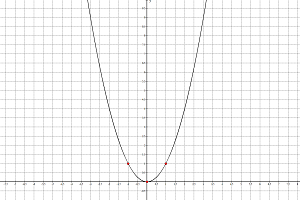
На малюнку зображена прямокутна система координат (XOY), екстремум, напрям гілок креслення функції вздовж осі абсцис.

Канонічне рівняння має вигляд:

y2 = 2 * p * x,

де коефіцієнт p – фокальний параметр параболи (AF).

В алгебрі воно запишеться інакше:

y = a x2 + b x + c (впізнаваний шаблон: y = x2).

Властивості та графік квадратичної функції

Функція має віссю симетрії і центром (екстремум). Область визначення – все значення осі абсцис.

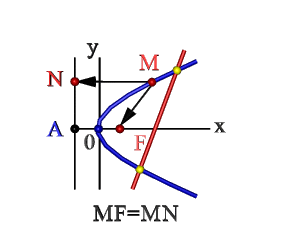
Область значень функції – (-∞, М) або (М, +∞) залежить від напряму гілок кривої. Параметр М тут означає величину функції у вершині лінії.

Як визначити, куди спрямовані гілки параболи

Щоб знайти напрям кривої такого типу з виразу, потрібно визначити знак перед першим параметром алгебраїчного виразу. Якщо а 0, то вони спрямовані вгору. Якщо навпаки – вниз.