Що таке парабола, канонічне рівняння, як знайти координати вершини параболи формула, побудова осі симетрії по квадратному рівнянню

Що таке парабола знають, мабуть, всі. А от як її правильно, грамотно використовувати при вирішенні різних практичних завдань, розберемося нижче.

Спочатку окреслимо основні поняття, які дає цьому терміну алгебра і геометрія. Розглянемо всі можливі види цього графіка.

Дізнаємося всі основні характеристики цієї функції. Зрозуміємо основи побудови кривої (геометрія). Навчимося знаходити вершину, інші основні величини графіка даного типу.

Дізнаємося, як правильно будується шукана крива по рівнянню, на що треба звернути увагу. Подивимося основне практичне застосування цієї унікальної величини в житті людини.

Що таке парабола і як вона виглядає

Алгебра: під цим терміном розуміється графік квадратичної функції.

Геометрія: це крива другого порядку, має ряд певних особливостей:

  1. Будь-яка пряма перетинає на площині шукану лінію в 2-х точках – так звані, «нулі» (крім основного екстремуму графіка).

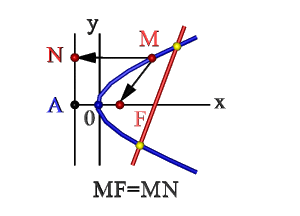
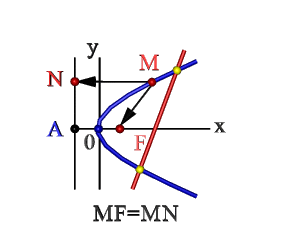
  2. Безліч точок площині ХОУ (М), відстань FM яких до F = відстані до прямої MN Де F – фокус, AN – директриса. Ці поняття розглянемо нижче.

Канонічне рівняння параболи

На малюнку зображена прямокутна система координат (XOY), екстремум, напрям гілок креслення функції вздовж осі абсцис.

Канонічне рівняння має вигляд:

y2 = 2 * p * x,

де коефіцієнт p – фокальний параметр параболи (AF).

В алгебрі воно запишеться інакше:

y = a x2 + b x + c (впізнаваний шаблон: y = x2).

Властивості та графік квадратичної функції

Функція має віссю симетрії і центром (екстремум). Область визначення – все значення осі абсцис.

Область значень функції – (-∞, М) або (М, +∞) залежить від напряму гілок кривої. Параметр М тут означає величину функції у вершині лінії.

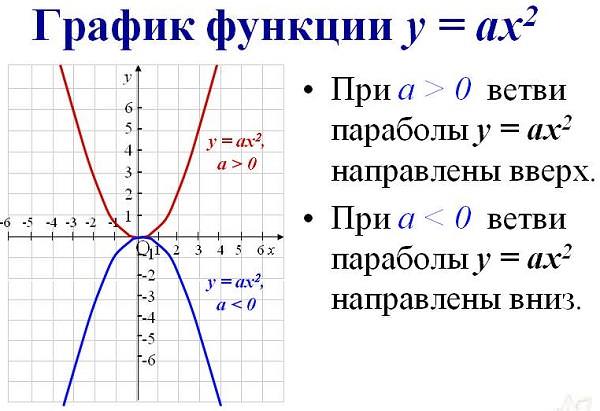
Як визначити, куди спрямовані гілки параболи

Щоб знайти напрям кривої такого типу з виразу, потрібно визначити знак перед першим параметром алгебраїчного виразу. Якщо а 0, то вони спрямовані вгору. Якщо навпаки – вниз.

Як знайти вершину параболи за формулою

Знаходження екстремуму є основним етапом при вирішенні багатьох практичних завдань. Звичайно, можна відкрити спеціальні онлайн калькулятори, але краще вміти робити самому.

Як її визначити? Є спеціальна формула. Коли b не дорівнює 0, треба шукати координати цієї точки.

Формули знаходження вершини:

  • x0 = -b / (2 * a);
  • y0 = y (x0).

Приклад.

Є функція у = 4 * x2 + 16 * x – 25. Знайдемо вершини цієї функції.

Для такої лінії:

  • х = -16 / (2 * 4) = -2;
  • y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Отримуємо координати вершини (-2, -41).

Зміщення параболи

Класичний випадок, коли у квадратичної функції y = a x2 + b x + c, другий та третій параметри дорівнюють 0, а = 1 – вершина знаходиться у точці (0; 0).

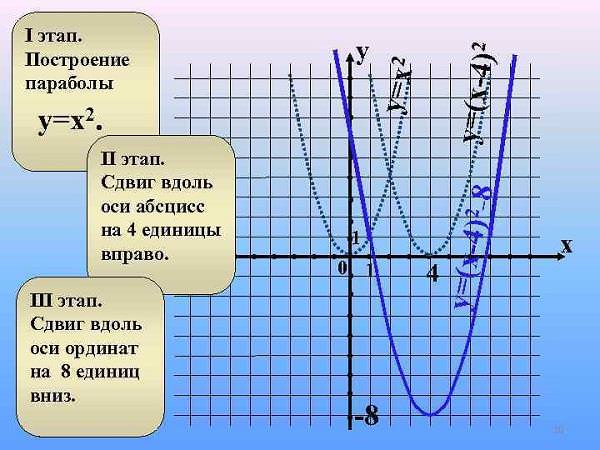
Дивіться також:  Визначення, ознаки і властивості довільній, равнобедренной і прямокутної трапеції

Рух по осях абсцис або ординат обумовлено зміною параметрів b і c відповідно. Зсув лінії на площині буде здійснюватися рівно на ту кількість одиниць, чому дорівнює значення параметра.

Приклад.

Маємо: b = 2, c = 3.

Це означає, що класичний вигляд кривої зрушиться на 2 одиничних відрізки по осі абсцис і на 3 — по осі ординат.

Як будувати параболу по квадратному рівнянню

Школярам важливо засвоїти, як правильно накреслити параболу за заданими параметрами.

Аналізуючи вирази та рівняння, можна побачити наступне:

  1. Точка перетину шуканої лінії з вектором ординат буде мати значення, рівне величині с.
  2. Всі точки графіка (по осі абсцис) будуть симетричні щодо основного екстремуму функції.

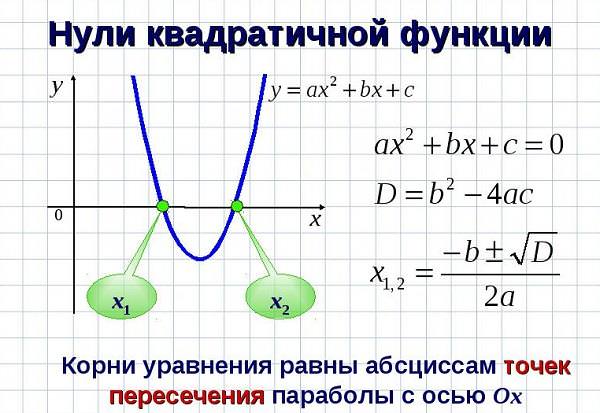
Крім того, місця перетину з ОХ можна знайти, знаючи дискриминант (D) такої функції:

D = (b2 — 4 * a * c).

Для цього потрібно прирівняти вираз до нуля.

Наявність коренів параболи залежить від результату:

  • D 0, х1, 2 = (-b ± D0,5) / (2 * a);
  • D = 0, х1, 2 = -b / (2 * a);
  • D 0, то нема точок перетину з вектором ОХ.

Отримуємо алгоритм побудови параболи:

  • визначити напрям гілок;
  • знайти координати вершини;
  • знайти перетин з віссю ординат;
  • знайти перетин з віссю абсцис.

Приклад 1.

Дана функція у = х2 — 5 * х + 4. Необхідно побудувати параболу. Діємо за алгоритмом:

  1. а = 1, отже, гілки спрямовані вгору;
  2. координати екстремуму: х = — (-5) / 2 = 5/2; y = (5/2)2 — 5 * (5/2) + 4 = -15/4;
  3. з віссю ординат перетинається в значенні = 4;
  4. знайдемо дискриминант: D = 25 — 16 = 9;
  5. шукаємо корені:
  • Х1 = (5 + 3) / 2 = 4; (4, 0);
  • Х2 = (5 — 3) / 2 = 1; (1, 0).

За отриманими точкам можна побудувати параболу.

Приклад 2.

Для функції у = 3 * х2 — 2 * х — 1 потрібно побудувати параболу. Діємо за наведеним алгоритмом:

  1. а = 3, отже, гілки спрямовані вгору;
  2. координати екстремуму: х = — (-2) / 2 * 3 = 1/3; y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3;
  3. з віссю у буде перетинатися у значенні у = -1;
  4. знайдемо дискриминант: D = 4 + 12 = 16. Значить коріння:
  • Х1 = (2 + 4) / 6 = 1; (1;0);
  • Х2 = (2 — 4) / 6 = -1/3; (-1/3; 0).

За отриманими точкам можна побудувати параболу.

Директриса, ексцентриситет, фокус параболи

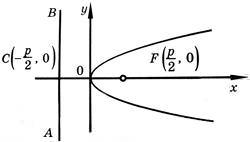
Виходячи з канонічного рівняння, фокус F має координати (p/2, 0).

Пряма АВ – директриса (свого роду хорда параболи певної довжини). Її рівняння: х = -р/2.

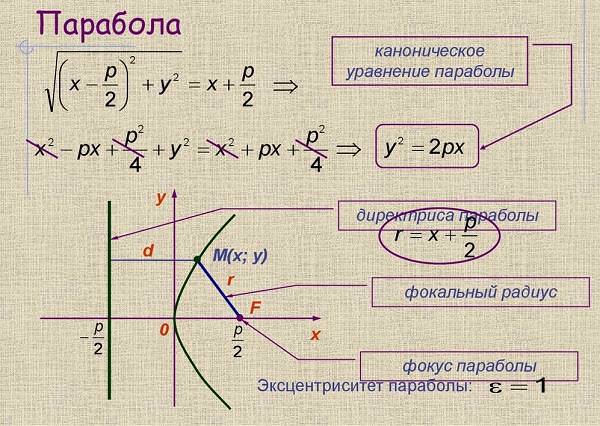
Ексцентриситет (константа) = 1.

Висновок

Ми розглянули тему, яку вивчають школярі в середній школі. Тепер ви знаєте, дивлячись на квадратичну функцію параболи, як знайти її вершину, в яку сторону будуть спрямовані гілки, є зміщення по осях, і, маючи алгоритм побудови, зможете накресліть її графік.