Часто, при вирішенні завдань, пов’язаних із спостереженнями та присвоєнням значення певної події за певний проміжок часу, виходить ряд чисел, який називається арифметичною прогресією.
Одна з головних відмінних особливостей — така математична модель має закономірність, за якою можна обчислити будь невідомий член, що спрощує прогнозування при обчисленні фізичних ситуацій.
Прикладами повсякденного використання можуть бути спостереження за температурою повітря, прогнозування витрат з занесенням результатів у таблицю та ін.
Визначення і приклади арифметичної прогресії
Це послідовність чисел, де кожне наступне число ряду (починаючи з другого) збільшується або зменшується на певну суму, що є константою.
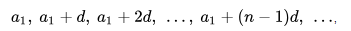
Крім цього для опису використовується ряд супутніх термінів і визначень. Членом (ап) називається одиничне число послідовності.
Різницею (d) називається фіксоване число, на яке збільшується або зменшується наступне число прогресії.

Крім цього, існують види таких рядів:
- зростаюча – числа ряду збільшуються за своїм значенням;
- щербатий – кожне наступне число ряду зменшується.
В якості прикладу наведемо послідовність чисел«3, 9, 15, 21, 27». Даний випадок – цей ряд чисел підпадає під характеристику арифметичної прогресії. Цей висновок робиться у тому випадку, коли різниця між членами ряду фіксована і дорівнює 6.