Другим після прямої важливим елементом просторової геометрії є площина. Вміння описувати її рівнянням дає можливість обчислення просторових кутів і висот для різних об’ємних фігур. У цій статті наведемо всі види рівнянь, що описують площину в просторі. Також розглянемо можливі варіанти взаємного розташування площин.

Геометричне поняття про площині

У двовимірної геометрії площину не розглядається, оскільки всі завдання вирішуються тільки в координатах x і y. Коли ж ми додаємо третю координатну вісь z, то площина стає важливим геометричним елементом.

Під поняттям “площину” розуміють сукупність точок, будь-які дві з яких якщо з’єднати, то отриманий вектор буде завжди перпендикулярний деякому заданому вектору. Цей заданий вектор називається нормаллю. Нормаль відіграє важливу роль при кількісному описі площині, а її властивості використовуються для вирішення різних завдань.

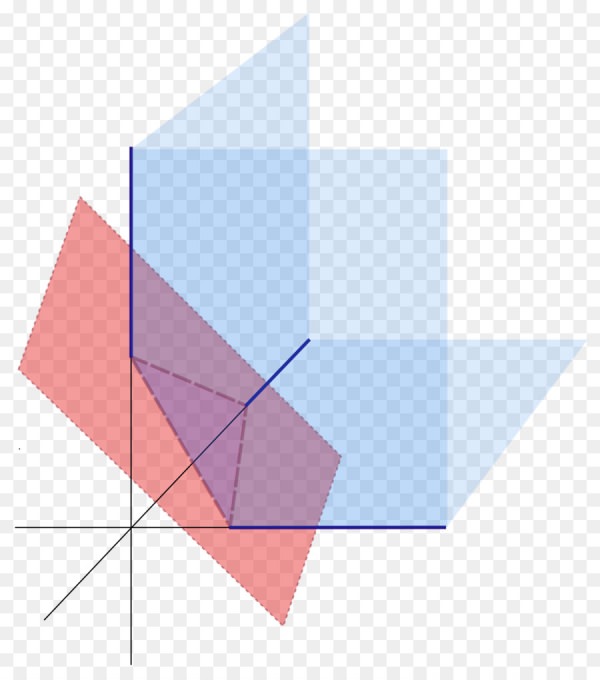
Малюнок нижче показує три площини у просторі (сині), які перетинає четверта (червона).