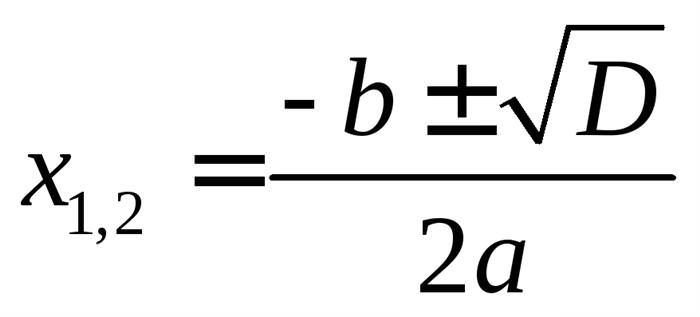У різних практичних діяльності людини на кшталт фізики, техніки, архітектури та інших точних наук, часто зустрічаються задачі з математичними моделями, який є рівняння, що мають змінну (x) в іншій мірі. Саме вони допомагають вченим у вивченні зовнішнього середовища та її використанні.
Квадратні рівняння
Квадратним називається рівняння виду ax2 + bc + c = 0, де x є зміною a (перший коефіцієнт), b (другий) і c (вільний) — це дійсні числа, які повинні приводити в умові задачі. Потрібно пам’ятати при вирішенні, що a ≠ 0. Як вже зрозуміло, воно дуже відрізняється від лінійного рівняння, його вивчали у молодших класах школи.
Щоб зрозуміти, як вирішувати квадратні рівняння, потрібно уявити футбольне поле, довжина якого на 10 метрів більше його ширини, а площа дорівнює 380 квадратних метрів. Потрібно знайти ширину футбольного поля.
Нехай x-змінна — це певна ширина, тоді її довжина буде (х +10) метрів. Потім x * (x + 10) = 380, адже дана площа 380 квадратних метрів в умові задачі, тобто x2 + 10x — 380 дорівнює нулю. Тут а = 1, b = 10, а c = -375 Це був один із прикладів квадратних рівностей.
Розрізняють два види рівнянь:
- Наведені — це випадок, коли в квадратному рівність a = 1.
- Неприведенные якщо a ≠ 1.
При цьому x2 — наведене, а вже при 5×2 воно стане неприведенным.
Поняття дискриминант
Існує певна система розв’язання таких рівнянь. Щоб знайти парний корінь такої рівності, досить запам’ятати наведену нижче формулу квадратного рівняння.
Буква D — це дискриминант. Звучить складно, але не варто лякатися, адже з латинської мови слово перекладається, як різниця. Він дорівнює: D = b2 — 4 ac. Дотримуючись цього, можна записати, що (2ax + b)2 = D. Є певні правила, як треба вирішувати дискриминант:
-
Якщо D менше нуля, то дійсних коренів немає.
- У разі коли D дорівнює нулю, в рішенні виходить тільки один дійсний корінь, але є рідкісні випадки з двома, тобто можна писати при вирішенні у формулі або + або -.
- Якщо D більше нуля, то в рівнянні два дійсних кореня, то є і плюс, і мінус. Але щоб вкоротити рішення достатньо записати ±, замість двох варіантів вирішення завдання.
Приклад першого способу знаходження через формулу дискримінанта квадратного рівняння і правильним розкладанням чисел:
- 9х2-6х+1=0;
- D = (-6)2 — 4 × 9 ×1 = 0;
- D еквівалентний нулю;
- x = -6/2×9 = 1/3.
Як приклад можна показати зрівняння: -8×2 = 0, у якого b і с дорівнюють нулю. Або 2×2 — 3 = 0, b нічому не одно. У рівнянні -7×2 + 4×2 = 0 c дорівнює нулю.
Різні квадратні рівняння
Крім звичайних дискримінант, є і половинні. Їх шукають для рівностей, у яких другий коефіцієнт — це парне число, за формулою: D1 = 4 k2 — 4 ac = 4 (k2 — ac). Щоб робити менше помилок, краще використовувати формули з дужками. Завдяки цьому у відповіді виходить чверть дискримінанта.
Квадратні рівності з комплексними змінними майже нічим не відрізняються від площини дійсних чисел і тим, які повинні проходити у восьмих класах. І щоб без проблем вирішувати їх, потрібно використовувати формулу.
Якщо в квадратному рівність хоча б один із загальних коефіцієнтів квадратного тричлена B або C дорівнює нулю, то таке рівняння називають неповним.
Отже воно буває лише трьох видів:
-
Рівняння виду ax2 дорівнює нулю. Оскільки a ≠ 0, маємо випадок, коли x2 = 0, коренем якого є число нуль. Як вже зрозуміло, є єдиний корінь х дорівнює нулю.
- ax2 + c дорівнює нулю, тоді не буде дорівнювати нулю. Щоб це краще зрозуміти, наводиться рівняння ах2 = -c, x2 = -c/a. Оскільки c ≠ 0 тоді і -з/а також не дорівнює нулю. Якщо -з/а більше нуля, то виходить два кореня: х1 = — корінь із -с/а і ще х2 = корінь зі з/а. Також можна написати замість мінуси і плюси одне рівняння із знаком: ±. Можливий випадок, коли ситуація є зворотним (з/а < 0), тоді коренів зовсім немає. Приклад: -2х2 + 50 дорівнює нулю. -2х2= -50; х2 = 25; х1,2 = ±5.
- ах2 + bx = 0, і при цьому b не дорівнює нулю. Розкладемо ліву частину рівняння на множники і вирішимо отримане х * (ах + b) = 0. Відповідь: x дорівнює нулю або ax + b = 0, а x = -b/a, оскільки a ≠ 0. У підсумку має вийти два кореня: х1 = 0, х2 = -b/a. Один із прикладів: 2х2 + 5х еквівалентний нулю; х(2х+ 5) = 0; х= 0 або 2х + 5 = 0. На даний момент очевидно, що x2 = -2,5 і х1 еквівалентний нулю.
З історії математики
Неповні квадратні рівності і деякі види невідомих коренів вавилонські математики вміли вирішити і створити ще 4000 років тому. Такі твори в Стародавній Греції вирішували тим же способом. Люди, що володіють знаннями точних наук, вирішували деякі квадратні рівняння геометричними прийомами.
Це показав давньогрецький вчений Діофант. Багато уваги таким рівнянням також виділяв арабський математик Мухаммед Альхорезми. Він знайшов як розв’язувати рівняння видів: ах2=bx; ax2=c; ax2+bx=c; ax2+c=bx; bc+c=ax2 і отримав позитивні коріння.
Формули, що зв’язують між собою коріння рівності і його коефіцієнти, що вперше знайшов французький математик Франсуа вієта які були введені в 1591 році. Його укладення в сучасних позначеннях мають вигляд: (а + b)x — x2 = 0.
Після швидкої публікації роботи нідерландського математика Жераром, а також француза Декарда і англійця Ньютона рівність коренів квадратного рівняння набуло сучасного вигляду.
| Рівняння | х1 і х2 | х1+х2 | х1×х2 |
| х2 -6х + 8 = 0 | 2 і 4 | 6 | 8 |
| x2+x-12=0 | -4 і 3 | -1 | -12 |
| x2-4x-5=0 | -3 -2 | -5 | 6 |
| x2-4x-5=0 | -1 5 | 4 | -5 |
Зараз мова йде про теорему Вієта, на яку треба звернути увагу. Її так називають через відомого французького математика Франсуа Вієта, яким і було відкрито цю властивість. Сума коренів зведеного квадратного рівності одно іншому коефіцієнта, взятого з негативним знаком, а добуток коренів — вільному члену. Часто записують у такому вигляді: х2 + px + q дорівнює нулю.
Теорему можна сформулювати так.
Якщо х1 і х2 — корені зведеного квадратного рівності х2+px+q еквівалентні нулю, то х1 + х2 = -p; x1 * x2 = q. Оскільки a ≠ 0, поділимо обидві частини рівняння на а і виходить сучасна формула: x2 — b/a * x + c/a дорівнює нулю.
