У фізиці закон Гаусса про потік вектора напруженості електричного поля є правилом, що зв’язує розподіл зарядів. Розглянута поверхня може бути закритою, охоплює обсяг, такий, як сферична поверхня.

Вперше закон був сформульований Жозеф-Луї Лагранж в 1773 році, а потім Карлом Фрідріхом Гауссом у 1813 році в контексті тяжіння еліпсоїдів. Це одне з чотирьох рівнянь Максвелла, що лежать в основі класичної електродинаміки. Закон Гаусса можна використовувати для виведення закону Кулона і навпаки.

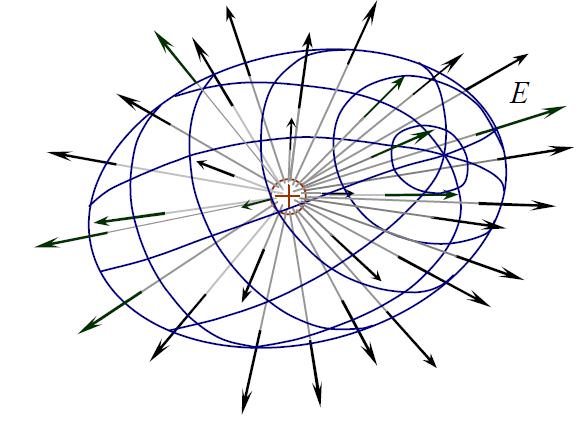
Математичний аспект

Закон Гаусса має математичне схожість з низкою законів в інших областях фізики, таких, як теорії магнетизму і гравітації. Фактично, будь-який закон зворотних квадратів можна сформулювати аналогічно закону Гауса. Наприклад, він сам по суті еквівалентний закону Кулона зворотного квадрата.

Закон може бути виражений математично з використанням векторного числення в інтегральній формі та диференціальній формі; обидва еквівалентні, так як вони пов’язані теоремою расходимости, також званої теореми Гауса. Кожна з цих форм, у свою чергу, також може бути виражена двома способами: в термінах залежності між електричним полем E і повним електричним зарядом або в термінах поля електричного зміщення D і вільного електричного заряду.