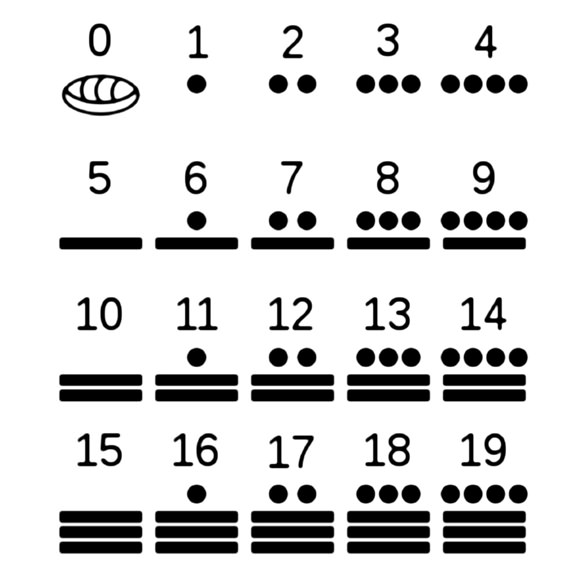
Якщо говорити самим простою мовою, система числення – це спосіб представлення чисел. Ми звикли використовувати при підрахунку метод, основою якого є 10. Інші системи числення, наприклад, мають підставу 16 (шістнадцяткова), 8 (вісімкова) і 2 (двійкова).

Доісторичні часи

Подібно до того, як перші спроби писати з’явилися після розвитку мовлення, перші зусилля по графічному представленню чисел з’явилися після того, як люди навчилися рахувати. Ймовірно, самий ранній спосіб вести підрахунок – це певна система рахунки фізичних об’єктів, таких як галька або палички. Судячи за звичаями нинішніх корінних народів, а також найдавнішим слідах письмових або скульптурних знахідок, найдавніші цифри представляли собою прості надрізи на дощечках, подряпини на камені, позначки на шматку металу і т. п. Не маючи фіксованих одиниць вимірювання, ніяких монет, ніякої торгівлі крім самого примітивного бартеру, ніякої системи оподаткування і ніяких потреб, крім тих, які підтримували життя, люди не потребували письмових цифрах до початку так званих історичних часів.