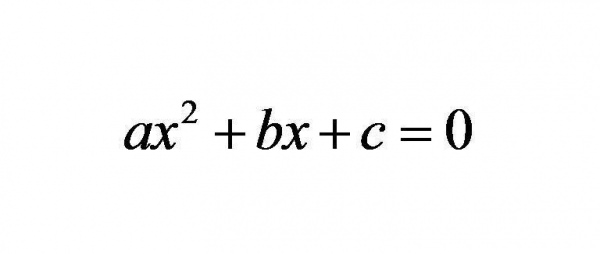Квадратні рівняння часто з’являються під час вирішення різних задач фізики і математики. У даній статті ми розглянемо, як вирішувати ці рівності універсальним способом “через дискриминант”. Приклади використання отриманих знань також даються в статті.

Про які рівняннях піде мова?

На рисунку зображена формула, в якій x – невідома змінна, а латинські символи a, b, c представляють собою деякі відомі числа.

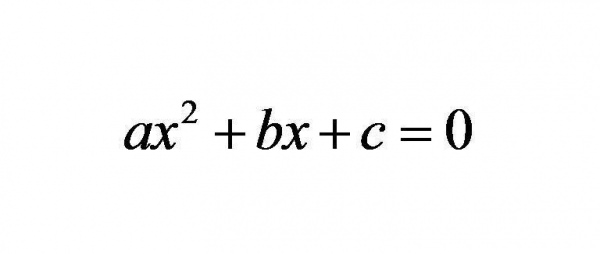
Кожен з цих символів називається коефіцієнтом. Як можна помітити, число “a” стоїть перед змінної x, піднесеної до квадрату. Це максимальна ступінь представленого вираження, тому воно називається квадратним рівнянням. Часто використовують інша його назва: рівняння другого порядку. Саме значення a – це квадратний коефіцієнт (стоїть при змінній в квадраті), b – це лінійний коефіцієнт (він знаходиться поруч із змінною, зведеної у першу ступінь), нарешті, число c – вільний член.

Зазначимо, що вигляд рівняння, який зображений на малюнку вище, є загальним класичним квадратним виразом. Крім нього існують інші рівняння другого порядку, в яких коефіцієнти b, c можуть бути нульовими.

Коли ставлять завдання вирішити цю рівність, то це означає, що такі значення змінної x потрібно знайти, які б йому задовольняли. Тут насамперед потрібно запам’ятати наступну річ: оскільки максимальна ступінь ікси – це 2, то даний тип виразів не може мати більше, ніж 2 рішення. Це означає, що якщо при рішенні рівняння були знайдені 2 значення x, які йому задовольняють, то можна бути впевненим, що не існує ніякого 3-го числа, підставляючи яке замість x, рівність також би було істиною. Рішення рівняння в математиці називають його корінням.