Розділ фізики, відповідальний за вивчення особливостей руху в просторі тіл, називається кінематикою. У цій статті розглянемо, які фізичні величини в кінематиці використовуються для опису переміщень об’єктів, а також розкриємо, що таке прискорення.

Фізичні величини в кінематиці

Коли тіло рухається в просторі, то нам важливо знати, яку відстань вона проходить за вказаний проміжок часу і вздовж якої траєкторії рухається.

Для опису пройдених відстаней у фізиці використовують поняття шляху – L. У випадку руху по колу замість шляху користуються поняттям кута повороту – θ. Величину L в СІ вимірюють в метрах (м), а величину θ – в радіанах (рад.).

Крім шляху важливо знати також швидкість руху тел. Під нею розуміють швидкість проходження відстаней. Математичний вираз для лінійної швидкості приймає вигляд:

v = d L / d t

Для опису руху по колу застосовують кутову швидкість ω, яка розраховується так:

ω = d θ / d t

Третьою важливою величиною кінематики є прискорення.

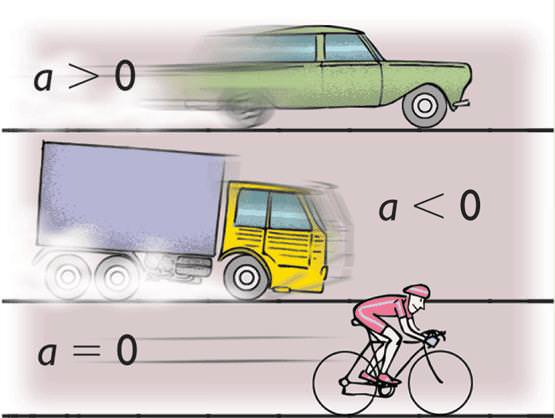
Що таке прискорення? Це величина у фізиці, яка показує, як швидко змінюється швидкість у часі. Математично це можна записати так:

a = d v / d t

Якщо підставити в цю формулу прискорення вираз для швидкості, отримаємо:

a = d2 L / d t2

Прискорення – це перша похідна від швидкості за часом або друга похідна по часу пройденого шляху.