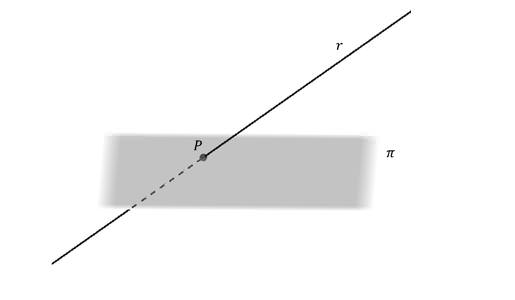
При вивченні шкільного курсу геометрії в двовимірному просторі велике час приділяють розгляду поведінки прямих. Коли ж переходять до вивчення стереометрії в старших класах, то на перший план виходять теми площин і прямих у просторі. Дана стаття присвячена одному з таких питань. А саме темі обчислення між площинами і прямими кутів і відстаней.
Пряма на площині та способи задавання
Щоб з успіхом вирішувати задачі обчислення між прямими і площинами кутів і відстаней, необхідно навчитися математично задавати ці геометричні об’єкти, а також оволодіти методами роботи з відповідними рівняннями. Почнемо з постановки прямих на площині.
Кожен школяр знає наступну формулу:
y = k*x + b
Працювати з нею досить зручно в двовимірному просторі. Її легко використовувати, щоб накреслити пряму в прямокутній системі координат. Крім того, знання коефіцієнта k для кожної з них дозволяє сказати, чи вони будуть паралельні, або ж вони перетинаються (для паралельних їх коефіцієнти k дорівнюють).
Якщо записати наведене вираз в дещо іншому вигляді, то вийде формула загального типу для прямої. Її форма наступна:
A*x + B*y + C = 0
Очевидно, що за допомогою простих перетворень можна отримати з неї перше вираження.
Записані формули можна застосовувати також для обчислення кута перетину прямих. Однак для цього необхідно провести ряд перетворень, що є незручним. Тому, коли в задачі потрібно знайти який-небудь кут, краще користуватися векторною формою подання прямій. Її вигляд можна записати так:
(x; y) = (x0; y0) + λ*(a; b)
У цьому рівність координати ікс та ігрек з нульовими індексами описують стан деякої точки, через яку пряма проходить. Значення a і b є координатами вектора, що лежить на ній. Він може бути спрямований в один бік прямої, так і в іншу, пряма від цього не змінюється. Зазначений вектор прийнято називати напрямних, оскільки він однозначно визначає поширення прямої на площині. Лямбда λ – це параметр, який приймає довільне значення з безлічі дійсних чисел.
Звертаємо увагу, що векторна форма запису тим і чудова, що містить явно спрямований відрізок прямої, координати якого використовуються для визначення кута між двома прямими на площині.