Будь-яке тверде тіло в тривимірному просторі має деяким обсягом. Обчисленням цієї характеристики геометричних фігур займається стереометрія. У цій статті розглянемо, що таке трикутна призма, і за якою формулою об’єм трикутної призми може бути розрахований.

Трикутна призма

Ця фігура відноситься до класу призм, тому вона, як будь-який представник цього класу, складається з двох однакових паралельних підстав і паралелограмів. Підставами є трикутники довільного типу (рівносторонні, рівнобедрені, прямокутні та інші), бічні сторони можуть бути довільними параллелограммами, ромбами, квадратами і прямокутниками. Число бічних сторін дорівнює трьом. Малюнок нижче демонструє, про який фігурі піде мова.

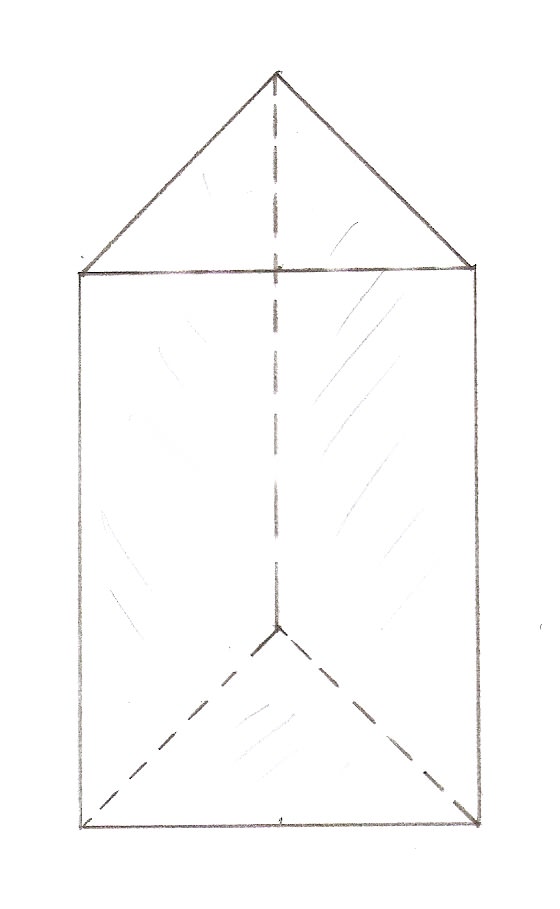
На цьому малюнку ми бачимо геометричну фігуру, яка складається з п’яти сторін, дев’яти ребер і шести вершин. Сторони ми вже охарактеризували. Що стосується ребер, то будь-яку з них можна віднести до одного з двох типів: або ребро належить одному з підстав (у цьому випадку воно є стороною трикутного підстави), або воно утворене перетинанням бічних граней (бічне ребро). Важливою властивістю призми є рівність всіх її бічних ребер.

Всі трикутні призми класифікуються за двома ознаками:

• прямі і похилі;
• правильні і неправильні.

Пряма призма має прямокутними бічними сторонами. Якщо її заснування будуть рівносторонніми трикутниками, тоді вона буде правильною. Далі ми наведемо формули об’єму призми трикутної прямий, правильної фігури, призми з прямокутним трикутником і фігури похилій.