Динаміка обертання є одним із важливих розділів сучасної механіки, яка розглядає закони обертального переміщення тіл навколо осей і точок. У даній статті ми детально вивчимо головне рівняння динаміки обертання – рівняння моментів.

Момент імпульсу

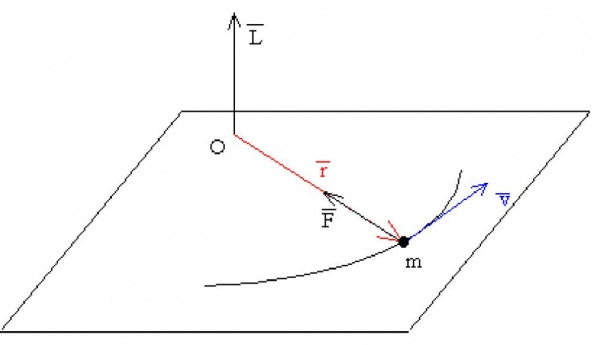
Кожному школяреві відомо, що являє собою механічний імпульс, який більш правильно називати кількістю руху. Тепер припустимо, що матеріальна точка, що має масу m, обертається навколо осі O з лінійною швидкістю v. Якщо радіус обертання позначити як r, тоді можна записати наступний вираз:

L = [m*v*r].

Перші два множника у правій частині рівності є лінійним імпульсом точки. Векторне твір цього імпульсу на вектор r, спрямований від осі обертання до точки, називається моментом імпульсу L.

Величина L є векторною. Спрямована перпендикулярно площині обертання точки. Напрямок моменту імпульсу матеріальної точки визначається за допомогою правила правої руки правила буравчика. Обертання точки проти годинникової стрілки створює позитивний момент імпульсу.

Оскільки швидкість обертання v спрямована по дотичній до кругової траєкторії, то векторне вираз можна переписати у скалярної формі:

L = m*v*r.