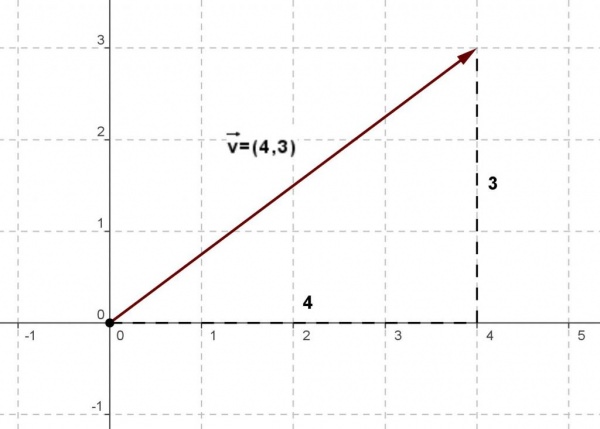
В математиці вектор – це напрямлений відрізок певної довжини. У фізиці під векторною величиною розуміють повну характеристику деякої фізичної величини, яка має модулем і напрямком дії. Розглянемо основні властивості векторів, а також приклади фізичних величин, які є векторними.

Скаляри та вектора

Скалярні величини в фізики є параметрами, які можуть бути виміряні і представлені одним числом. Наприклад, температура, маса і об’єм є скалярами, оскільки вони вимірюються числом градусів, кілограм і кубічних метрів відповідно.

У більшості ж випадків виявляється, що число, що визначає скалярну величину, не несе вичерпної інформації. Наприклад, розглядаючи таку фізичну характеристику, як прискорення, буде недостатньо сказати, що воно дорівнює 5 м/с2, оскільки потрібно знати, куди воно направлене, проти швидкості руху тіла, під деяким кутом до цієї швидкості або інакше. Крім прискорення, прикладом векторної величини в фізики є швидкість. Також в цю категорію входять сила, напруженість електричного поля і багато інші.

Згідно з визначенням векторної величини як спрямованого в просторі відрізка, вона може бути представлена у вигляді набору чисел (компонент вектора), якщо її розглядати у певній системі координат. Найчастіше у фізиці та математиці, виникають завдання, які для опису вектора вимагають знання його двох (задачі на площині) або трьох (задачі в просторі) компонентів.