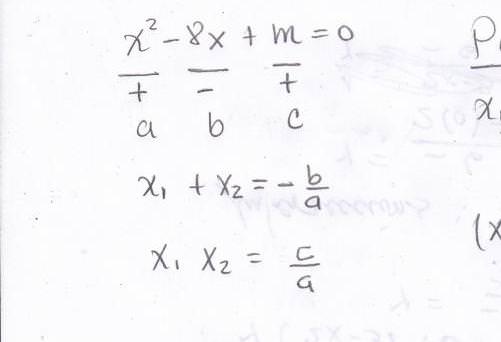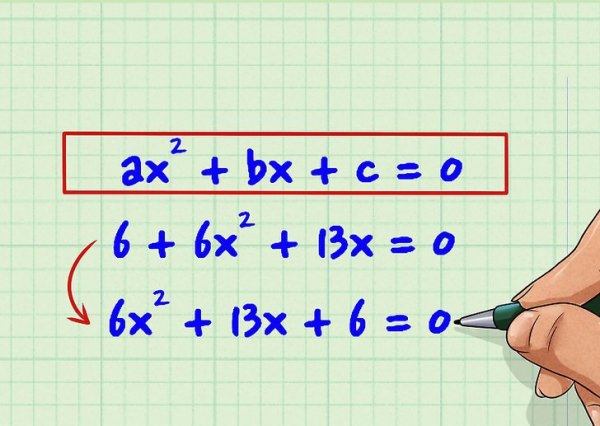При вивченні способів вирішення рівнянь другого порядку в шкільному курсі алгебри, розглядають властивості отриманих коренів. Вони в даний час відомі під назвою теореми Вієта. Приклади використання її наводяться в даній статті.

Квадратне рівняння

Рівняння другого порядку являє собою рівність, яке показано на фото нижче.

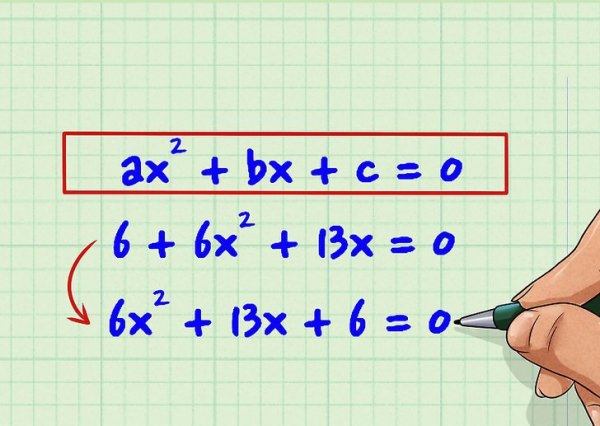
Тут символи a, b, c є деякими числами, які носять назву коефіцієнтів розглянутого рівняння. Щоб вирішити рівність, необхідно знайти такі значення x, які роблять його справжнім.

Зауважимо, що оскільки максимальне значення ступеня, у яку зводиться ікс, дорівнює двом, тоді число коренів в загальному випадку також дорівнює двом.

Для рішення цього типу рівностей існує кілька способів. У цій статті розглянемо один з них, який передбачає використання так званої теореми Вієта.

Формулювання теореми Вієта

В кінці XVI відомий математик Франсуа вієта які були введені (француз) зауважив, аналізуючи властивості різних коренів квадратних рівнянь, що певні їх комбінації задовольняють конкретним співвідношенням. Зокрема, цими комбінаціями є їх добуток і сума.

Теорема Вієта встановлює наступне: корені квадратного рівняння при їх сумі дають відношення коефіцієнтів лінійного до квадратичним взяте з протилежним знаком, а при їх творі призводять до відношення вільного члена до квадратичним коефіцієнту.

Якщо загальний вигляд рівняння записано так, як це представлено на фото у попередньому розділі статті, тоді математично цю теорему можна записати у вигляді двох рівностей:

• r2 + r1 = -b / a;
• r1 х r2 = c / a.

Де r1, r2 – значення коренів розглянутого рівняння.

Наведені два рівності можна використовувати для вирішення ряду самих різних математичних задач. Використання теореми Вієта у прикладах з рішенням наведені в наступних розділах статті.