Будь-які переміщення тіл у просторі, траєкторія яких є окружністю, передбачають знання не тільки кутової швидкості, але і моменту інерції для опису цього руху. Що таке момент інерції, а також чому він рівний для стрижня і колеса, відповість дана стаття.

Обертання і момент інерції

Фізична величина, яка називається моментом інерції, позначається, як правило, буквою I і з’являється у фізиці при розгляді моменту імпульсу матеріальної точки, яка обертається навколо осі. Момент імпульсу L в скалярної формі записується наступним виразом:

L = r*m*v

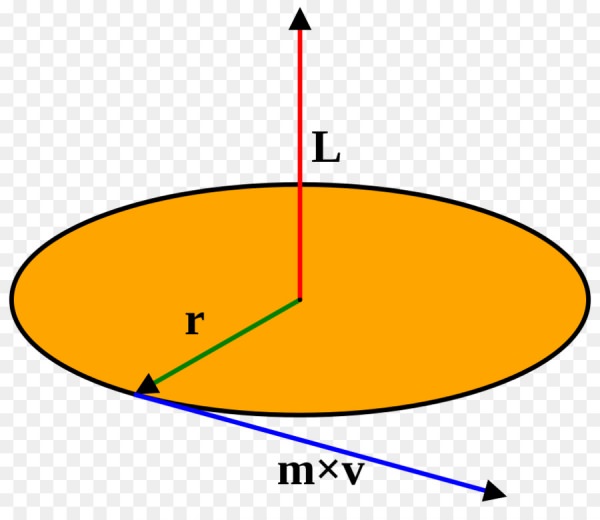
Тут r – відстань до осі матеріальної точки, m – її маса, v – лінійна швидкість. Використовуючи зв’язок останньої з кутовий швидкістю ω, отримуємо вираз:

L = r2*m*ω, де ω = v/r

Відповідаючи на питання про те, що таке момент інерції, слід сказати, що це величина I = r2*m. Тобто вона залежить від маси обертового об’єкта, швидко зростає із збільшенням відстані до осі і вимірюється в кг*м2.