Призма є геометричної об’ємною фігурою, характеристики та властивості якої вивчають у старших класах шкіл. Як правило, при її вивченні розглядають такі величини, як об’єм і площа поверхні. У даній же статті розкриємо дещо інше питання: приведемо методику визначення довжини діагоналей призми на прикладі чотирикутної фігури.

Яка фігура називається призмою?

В геометрії дається наступне визначення призмі: це об’ємна фігура, обмежена двома багатокутними однаковими сторонами, які паралельні один одному, і деяким числом паралелограмів. Малюнок нижче показує приклад призми, відповідає цьому визначенню.

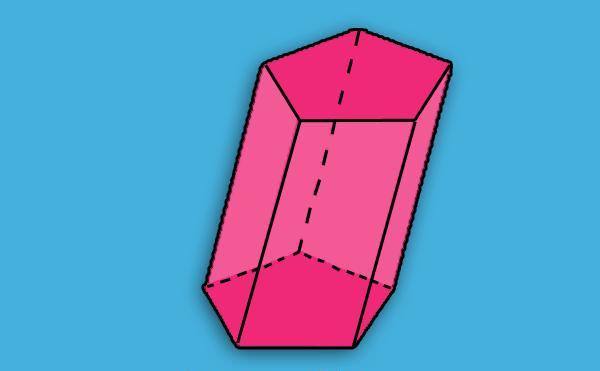
Ми бачимо, що два червоних п’ятикутника дорівнюють одна одній і перебувають у двох паралельних площинах. П’ять рожевих паралелограмів з’єднують ці пятиугольники в цілісний об’єкт – призму. Два п’ятикутника називаються підставами фігури, а її паралелограми – це бічні грані.

Призми бувають прямі і похилі, які також називають прямокутними і косоугольными. Різниця між ними полягає в кутах між підставою і бічними гранями. Для прямокутної призми всі ці кути рівні 90o.

За кількістю сторін або вершин багатокутника на підставі говорять про призмах трикутних, п’ятикутних, чотирикутних і так далі. Причому якщо цей багатокутник є правильним, а сама призма прямій, то таку фігуру називають правильною.

Наведена на попередньому малюнку призма є п’ятикутні похилій. Нижче ж зображена п’ятикутна пряма призма, яка є правильною.

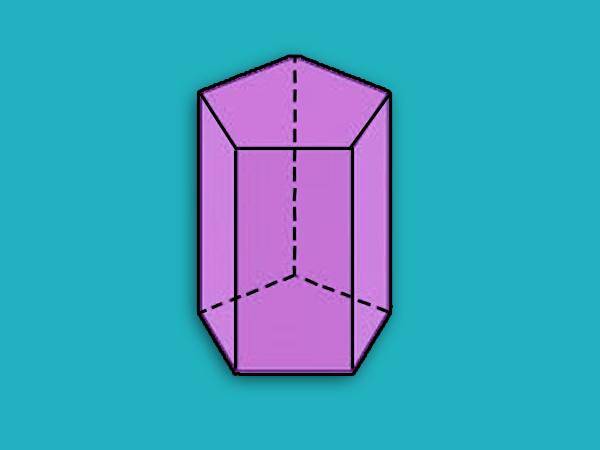
Всі обчислення, включаючи методику визначення діагоналей призми, зручно виконувати саме для правильних фігур.