Стереометрія – важливий розділ геометрії, що вивчає властивості фігур у тривимірному просторі. У цій статті з точки зору стереометрії розглянемо клас геометричних об’єктів, який називається призми, дамо визначення призми і перерахуємо її основні види та характеристики.

Що таке призма?

Перш ніж дати визначення призми, уявімо собі довільний багатокутник на площині. Скориставшись операцією паралельного перенесення цього багатокутника в просторі, ми отримаємо об’ємну фігуру. Ця фігура буде складатися з двох однакових багатокутників і декількох паралелограмів. Це і є призма довільної форми. Малюнок нижче показує, як виглядає шестикутна призма.

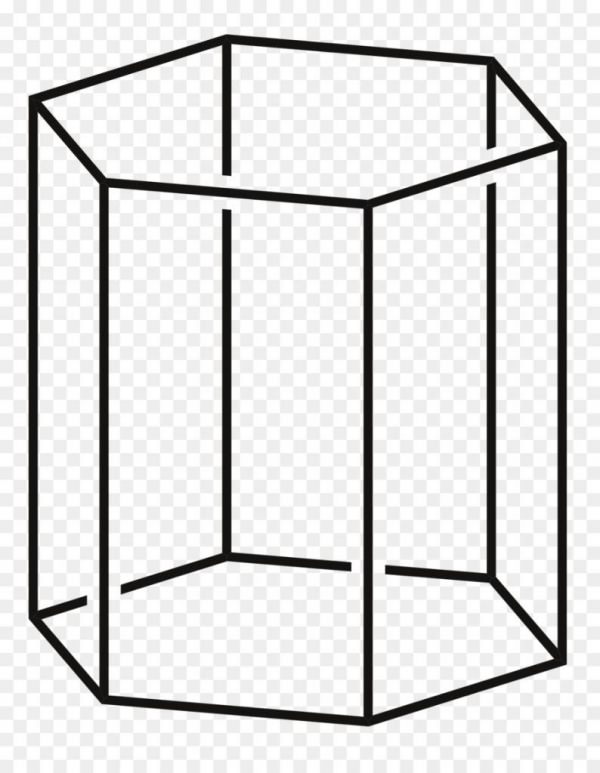
Таким чином, можна дати наступне визначення призми: це об’ємна фігура, яка утворена n параллелограммами і двома однаковими n-вугільними сторонами, розташованими в паралельних площинах. Однакові n-кутники називаються підставами фігури, а її паралелограми утворюють бічну поверхню.