Призма є однією з досконалих об’ємних фігур, поряд з кулею, циліндром і пірамідою, властивості якої розглядаються у спеціальному розділі геометрії – стереометрії. У цій статті обговоримо основні характеристики прямокутної призми.

Фігура призма

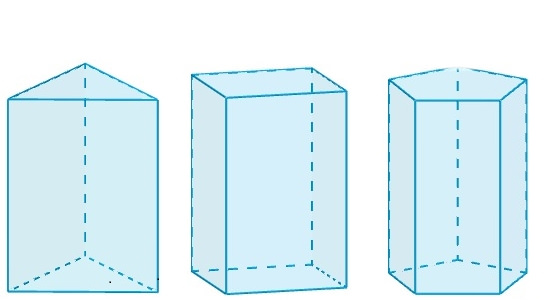
Багато знають про трикутні призми або шестикутні, але не кожна людина чітко уявляє, що це за фігура в загальному вигляді. В геометрії під нею розуміють просторовий об’єкт, який обмежений двома однаковими многокутниками і кількома чотирикутниками. Два багатокутника називаються основами призми. Вони лежать у паралельних площинах. Всі чотирикутники є параллелограммами і утворюють бічну поверхню фігури.

Основні формули і властивості призми стосуються питань визначення об’єму, площі її поверхні та числа утворюють фігуру елементів. До складу останніх входять вершини, ребра та грані. Кількості цих елементів пов’язані один з одним виразом Ейлера для поліедрів. Воно має наступний вигляд:

Число ребер = число граней + число вершин – 2

Оскільки бічна поверхня призми представлена завжди параллелограммами, то основні її характеристики залежать від типу багатокутника, що лежить в основі цієї фігури. Якщо гратки є трикутник, то призма називається трикутною, якщо чотирикутник – то чотирикутної і так далі.