Однією з об’ємних фігур, які вивчаються у курсі просторової геометрії, є піраміда. Важливою характеристикою цієї фігури є її висота. У статті дамо визначення висоти піраміди і наведемо формули, через які вона пов’язана з іншими лінійними характеристиками.

Що собою являє піраміда

Під пірамідою розуміють просторову геометричну фігуру, яка виходить в результаті з’єднання всіх кутів багатокутника з однієї точки простору. Малюнок нижче демонструє розташування ліній (ребер) для чотирикутної і п’ятикутні пірамід.

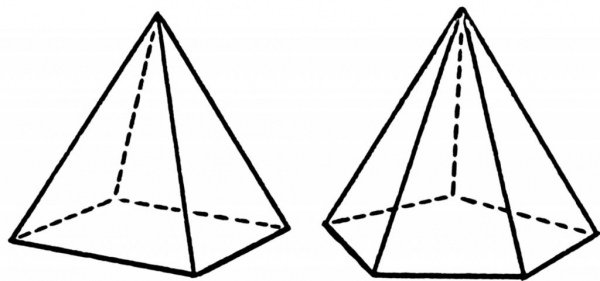
Багатокутна грань фігури називається її підставою. Точка, де всі трикутні грані з’єднуються, називається вершиною. Для визначення висоти піраміди зазначені елементи є важливими.

Висота фігури

Висотою піраміди називається перпендикуляр, який з її вершини опущений на площину підстави. Важливо розуміти, що з кожної вершини, що належить основи фігури, теж можна провести перпендикуляр до відповідної трикутної грані, однак він заввишки не буде. Висота піраміди – це єдиний перпендикуляр, який є однією з важливих її лінійних характеристик.

Кожному школяреві відомо, що будь-яка плоска фігура має геометричним центром (у фізиці йому відповідає центру мас). Наприклад, геометричний центр для довільного трикутника визначається точкою перетину його медіан, для паралелограма – точкою перетину діагоналей. Якщо висота піраміди перетинає її підставу в геометричному центрі, то фігура називається прямою. Піраміда пряма, що має в підставі багатокутник з однаковими сторонами і кутами, називається правильною.

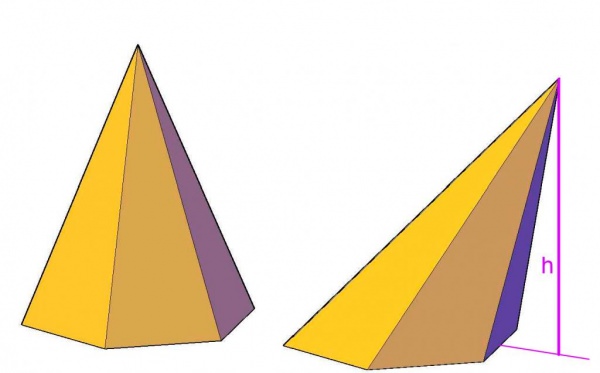
Малюнок вище показує, чим відрізняється неправильна піраміда від правильної. Видно, що висота фігури неправильної лежить за межами її заснування, в той час як у правильної шестикутної піраміди висота знаходиться всередині фігури, перетинаючи її підставу в геометричному центрі.

Важливими властивостями всіх правильних пірамід є наступні:

• всі бічні грані являють собою рівнобедрені трикутники і рівні один одному;
• довжини бічних ребер і апофем є однаковими.