Людська природа така, що він постійно прагне до досконалості геометричних форм створюваних ним творів. Вчинені фігури в просторі вивчає стереометрія. У цій статті розглянемо одну з них, яка називається призмою. Формули, що описують важливі властивості цієї фігури, також наводяться в статті.
Що таке призма?
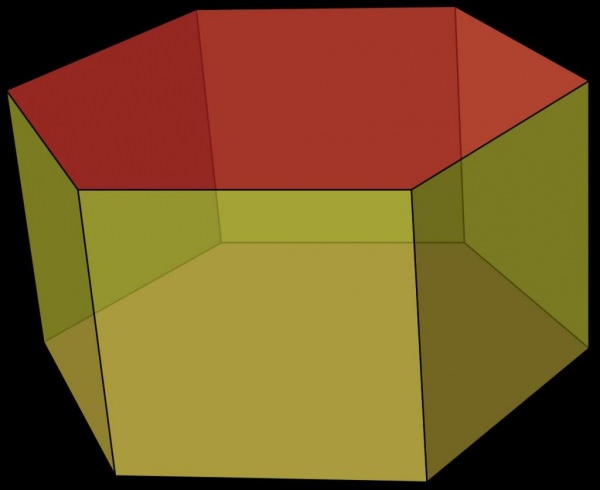
У стереометрії під названої фігурою розуміють просторовий об’єкт, обмежений двома однаковими багатокутними гранями, що знаходяться в паралельних площинах, і кількома параллелограммами, які з’єднують відповідні сторони многокутників в єдину фігуру.
Покажемо на прикладі шестикутної призми, як можна побудувати будь-яку з даного класу фігур. Припустимо, що у нас є плоский шестикутник. Він може бути правильним або неправильним. Тепер виберемо деякий вектор у просторі, який не буде знаходитися в площині шестикутника, і перемістимо на цей вектор весь шестикутник. У новій площині ми отримаємо шестикутник, аналогічний вихідного, а фігури, які вийшли у процесі паралельного перенесення, будуть параллелограммами. Кінцева об’ємна фігура показана нижче. Вона називається шестикутної призмою.
Які призми бувають?
Існує кілька видів розглянутих фігур, які важливо розглянути, оскільки форма описують різні властивості формул призм визначається типом останніх.
Залежно від багатогранника в основі призми бувають опуклими й увігнутими, трикутними, чотирикутними і так далі. В залежності від того, чи є всі паралелограми призми прямокутниками, говорять про похилих і прямих призмах. Спеціальний вид призм, вивчення властивостей якого приділяється належна увага в курсі стереометрії, – це правильні фігури, які від інших призм відрізняються тим, що їх основа є правильним гратки, і самі вони прямі. Набір таких фігур показаний нижче.
Далі наведемо формули об’єму призми, площі її поверхні і довжини діагоналей, беручи до уваги вигляд фігури.
Діагоналі призм
Діагоналями призми називають відрізки, які з’єднують будь-які два не сусідні вершини фігури. Діагоналі можуть розташовуватися в одній площині, наприклад в площині підстави або бічній грані, так і в обсязі призми. Трикутна призма є єдиною і розглянутого класу фігур, яка не має об’ємних діагоналей.
Не існує формул загального вигляду, які дозволяють розрахувати значення довжини тієї чи іншої діагоналі для призми довільного типу. Щоб знайти цю довжину, необхідно провести певний геометричний аналіз. Наприклад, для прямої чотирикутної призми з прямокутним підставою об’ємна діагональ обчислюється за формулою:
d = √(a2 + b2 + h2)
Де a, b, h – довжини сторін основи і висота фігури.
У разі правильної шестикутної призми, довжина діагоналі, яка з’єднує протилежні вершини різних підстав, обчислюється так:
d = √(4*a2 + h2)
Де h – також висота фігури, a – довжина сторони шестикутника.
Подібні формули можна записати для будь-якої діагоналі довільної призми.
Площа поверхні призми
Формулу для площі поверхні будь призми можна записати, якщо для початку зробити її розгортку і проаналізувати, з яких сторін складається вивчається фігура. Оскільки будь-яка призма має два n-вугільних підстави та n паралелограмів, значить, складаючи всі площі цих фігур, можна отримати шуканий результат.
Задача обчислення площі поверхні полегшується, якщо призма є прямою. У такій фігурі всі бічні сторони – це прямокутники, площа яких легко знайти, знаючи висоту фігури і довжини сторін основи.
Загальну для площі призм формулу можна привести тільки для випадку правильної фігури. Нагадаємо, що правильні призми складаються з рівносторонніх і равноугольных підстав і однакових прямокутників бічній поверхні. Для площі основи призми формула носить універсальний характер:
Sn = n/4*a2*ctg(pi/n)
Площа довільній бічній грані обчислюється так:
S1 = a*h
Тепер залишається скласти записані вирази, враховуючи кількість сторін фігури, щоб отримати шукану формулу для площі S всій поверхні призми:
S = 2*Sn + n*S1 = n/2*a2*ctg(pi/n) + n*a*h
Як видно, для обчислення величини S правильної призми достатньо знати довжину сторони основи, кількість його вершин і висоту фігури.
Якщо призма є похилій, то розрахувати для неї площа бічної поверхні можна, якщо обчислити периметр зрізу Psr, площина якого перпендикулярна всім бічним граням, а потім помножити цей периметр на довжину бічного ребра c. Тобто:
Sb = Psr*c
Додавши до величини Sb дві площі підстави So, ми отримаємо площу всієї поверхні S похилій фігури.
Обсяг фігури
Для будь-якої призми, незалежно від її виду, об’єм обчислюється за такою універсальною формулою:
V = So*h
Очевидно, що для правильної призми формула обсягу набуває вигляду:
V = n/4*a2*h*ctg(pi/n)
Що стосується похилих призм, то обсяг для них обчислити дещо складніше, оскільки необхідно спочатку визначити значення висоти h. Щоб це зробити, слід враховувати значення кутів між бічними гранями і ребрами і підставою.
