Пряма в геометрії є одним з найбільш важливих елементів, оскільки з неї збираються багато фігури як на площині, так і в просторі. Досить назвати трикутник, паралелограм, призму, піраміду – всі вони утворені пересічними прямими. У цій статті дано відповідь на запитання, як по двох точках скласти рівняння прямої.

Рівняння прямої для двовимірного та тривимірного випадків

Перш ніж переходити до обговорення питання, як по двох точках скласти рівняння прямої, слід зрозуміти, про що йде мова.

Під рівнянням прямої розуміють рівність, пов’язане з прийнятою системою координат, причому всі значення змінних, що задовольняють йому, повинні лягати на одну пряму. У двовимірному і тривимірному випадках це рівняння можна задати в наступному вигляді:

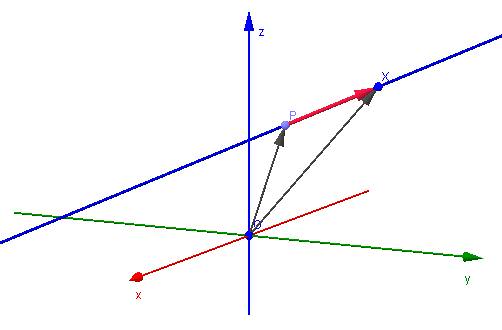
Q = P + α*u

Тут Q – координати довільної точки прямої, P – координати конкретної крапки, що належить прямій, u – напрямний вектор, α – будь-яке дійсне число. Направляючий вектор u є паралельним прямій. Цей вираз називається параметрично-векторним рівнянням.

У двовимірному випадку кожна точка на площині однозначно задається двома координатами x і y, тому можна записати рівняння прямої у вигляді:

(x; y) = (x0; y0) + α*(a; b)

Де (x0; y0) – координати відомої точки прямої, (a; b) – координати направляючого вектора. В параметричному вигляді це рівняння можна переписати як систему з двох рівнянь:

x = x0 + α*a;

y = y0 + α*b.

Висловлюючи параметр альфа і прирівнюючи отримані рівності, приходимо до виду:

y = b/a*x+(y0-x0*b/a) або

y = A*x + C, де A = b/a, C = (y0-x0*b/a)

Отриманий вираз знайоме кожному школяреві. Воно називається загальним рівнянням прямої на площині.

У просторі кожна точка задана не двома, а трьома координатами, тому її рівняння параметрично-векторне приймає форму:

(x; y; z) = (x0; y0; z0) + α*(a; b; c)

Параметрично-векторне рівняння зручно використовувати, коли потрібно скласти рівняння прямої, що проходить через дві точки.