Розглядом властивостей і особливостей правильних фігур в тривимірному просторі займається стереометрія. Одним з численних класів об’ємних фігур є призми. У цій статті наведемо формулу обсягу шестикутної призми і покажемо, як її слід використовувати при розв’язанні задачі.

Що таке шестикутна призма?

Коротко відповідаючи на поставлене питання, слід сказати, що будь-яка призма, що має в основі плоский багатокутник з шістьма кутами і шістьма сторонами, називається шестикутної. Цей багатокутник називається підставою фігури. Малюнок нижче показує, як виглядає така призма.

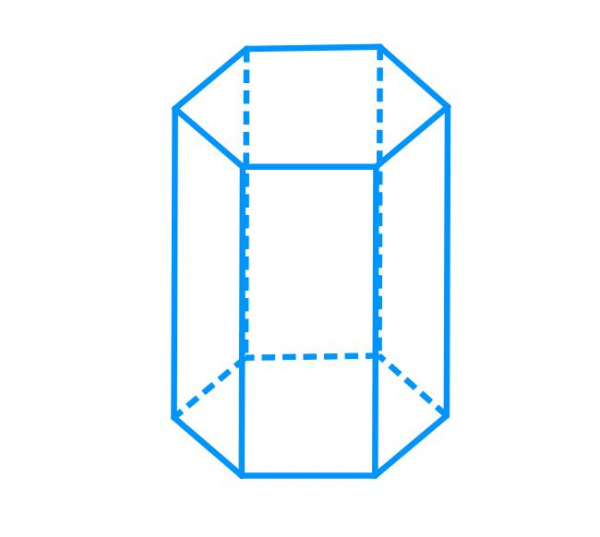
Видно, що фігура, утворена двома однаковими шестикутними підставами, які розташовані в паралельних площинах. З’єднані вони з допомогою шести паралелограмів. Призма має 8 граней, 18 ребер і 12 вершин.

Якщо всі паралелограми, які утворюють бічну поверхню, являють собою прямокутники або квадрати, то фігура буде прямою. У прямої призми відстань між підставами (висота) збігається з довжиною бічного ребра. Якщо підстави прямий фігури є рівносторонніми і равноугольными, то можна говорити про правильної шестикутної призми.