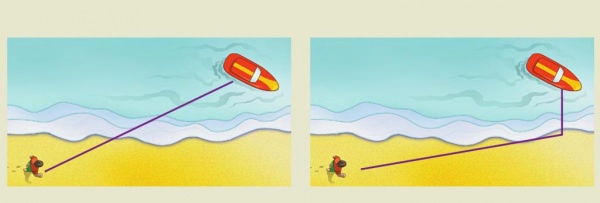
Поведінка світлових променів при їх проходженні через різні прозорі середовища можна однозначно визначити, не знаючи при цьому природи самого світла. Такими завданнями займається особливий розділ фізики – геометрична оптика. Закони її розглядаються в даній статті.

Властивості світлових променів в геометричній оптиці

Під властивостями променів у цьому розділі фізики розуміють особливості їх руху в прозорих середовищах. Зокрема, при переміщенні світлового пучка в гомогенної середовищі справедливі наступні твердження:

• траєкторією світла є пряма лінія;
• два світлові пучки, перетинаючись, не взаємодіють один з одним;
• речова середовище визначає швидкість руху світла в ній.

Ці властивості є фундаментальними для будь-якої електромагнітної хвилі. Завдяки їм виводяться основні закони геометричної оптики для явищ:

• відображення;
• заломлення.