Тіло кинули під кутом до горизонту: швидкість, дальність польоту і висота підйому

У цій статті розглянемо аналіз ситуації, коли тіло кинули під кутом до горизонту. Це може бути кидок каменю рукою, постріл снаряду з гармати, запуск стріли з лука і так далі. Всі названі ситуації описуються однаково з математичної точки зору.

Особливість руху під кутом до горизонту

У чому подібність названих вище прикладів з точки зору фізики? Воно полягає в характері діючих на тіло сил. Під час вільного польоту деякого тіла на неї діють дві сили:

  • Сила тяжіння.
  • Опір повітря.

Якщо маса тіла досить велика, а його форма є загостреною (снаряд, стріла), то опором повітря можна знехтувати.

Таким чином, рух кинутого під кутом до горизонту тіла – це задача, у якій фігурує тільки сила тяжіння. Саме вона і визначає форму траєкторії, яка з хорошою точністю описується параболічною функцією.

Рівняння руху по параболічної траєкторії. Швидкість

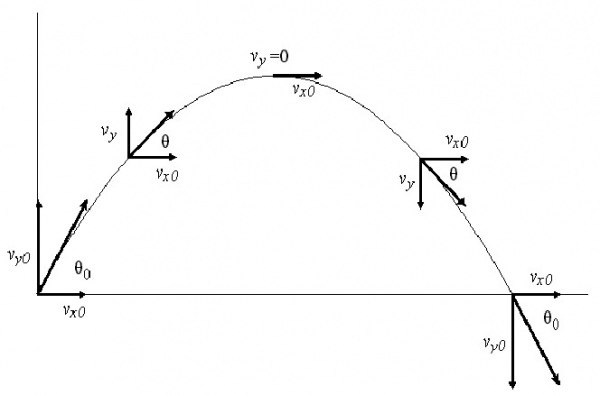
Тіло кинули під кутом до горизонту. Як можна описати його рух? Оскільки єдина діюча в процесі польоту тіла сила спрямована вниз, то її горизонтальна складова дорівнює нулю. Цей факт означає, що горизонтальне переміщення об’єкта однозначно визначається початковими умовами (кутом кидка або пострілу θ і швидкістю v). Вертикальне ж переміщення тіла – це яскравий приклад равноускоренного руху, де роль прискорення відіграє постійна g (9,81 м/с2).

Дивіться також:  Що таке архів? Значення, походження, синоніми

Враховуючи сказане вище, можна записати дві компоненти для швидкості летить тіла в момент часу t:

vx = v * cos(θ);

vy = v * sin(θ) – g * t

Як видно, компонента vx від часу не залежить і залишається постійною протягом всієї траєкторії польоту (наслідок відсутності зовнішніх сил у напрямку осі x). Компонента ж vy має максимум в початковий момент часу. А потім починає зменшуватися аж до того, що звертається в нуль в максимальній точці зльоту тіла. Після цього вона змінює знак і в момент падіння виявляється дорівнює модулю початкової компоненти vy, тобто v*sin(θ).

Записані рівняння дозволяють визначити швидкість тіла, кинутого під кутом до горизонту в будь-який момент t. Її модуль дорівнює:

v = √ (vx2 + vy2) = √ (v2 * cos2(θ) + v2 * sin2(θ) – 2 * v* sin(θ) * g * t + g2 * t2) =

= √ (v2 – 2 * v * sin(θ) * g * t + g2 * t2)

Сторінка: 1 2 3