Знання властивостей геометричних фігур дозволяє не тільки вирішувати теоретичні завдання, а також виконувати різні практично важливі розрахунки. Однією з таких фігур, властивості якої будуть розглянуті в цій статті, є конус. Що таке конус, які види його бувають, як знайти його площу і об’єм? Нижче докладно висвітлюються всі ці питання.

Загальне визначення конуса в геометрії

Стереометрія, яка займається вивченням характеристик фігур в тривимірному просторі, пропонує наступний відповідь на питання, що таке конус: це фігура, поверхня якої утворена сукупністю прямих відрізків, що з’єднують деяку точку простору з визначеної кривої на площині.

Зазначена точка простору називається вершиною конуса, прямі відрізки – це генератрисы фігури або її утворюють, а сама крива на площині – це директриса (напрямна).

Під назване визначення підходить цілий клас фігур, найвідомішими з яких є круглий, еліптичний, параболічного та гіперболічного конуси. Еліптична фігура показана нижче на малюнку.

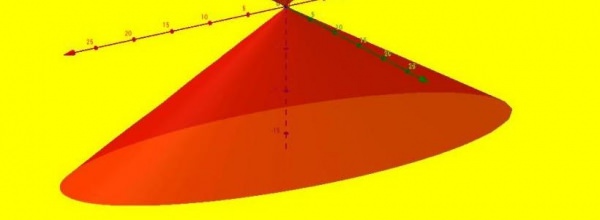
Директриса цього конуса являє собою замкнутий еліпс, який обмежує основа фігури. Генератрисы будь-якого конуса всі разом утворюють конічну поверхню, яка називається боковою. Ці дві поверхні (підстава і бічна) обмежують просторовий обсяг, який прийнято називати обсягом конуса.