Обертальний рух є не менш поширеним в природі, ніж лінійне переміщення об’єктів. Щоб переконатися в цьому, досить згадати обертання коліс автомобілів і велосипедів, лопатей вертольотів і вентиляторів, планет навколо своєї осі і навколо своїх зірок. Для опису процесу кругового переміщення об’єктів використовується фізична величина, яка отримала назву “момент імпульсу”. Розглянемо у статті, що вона собою являє.

Момент імпульсу частинки і вісь обертання

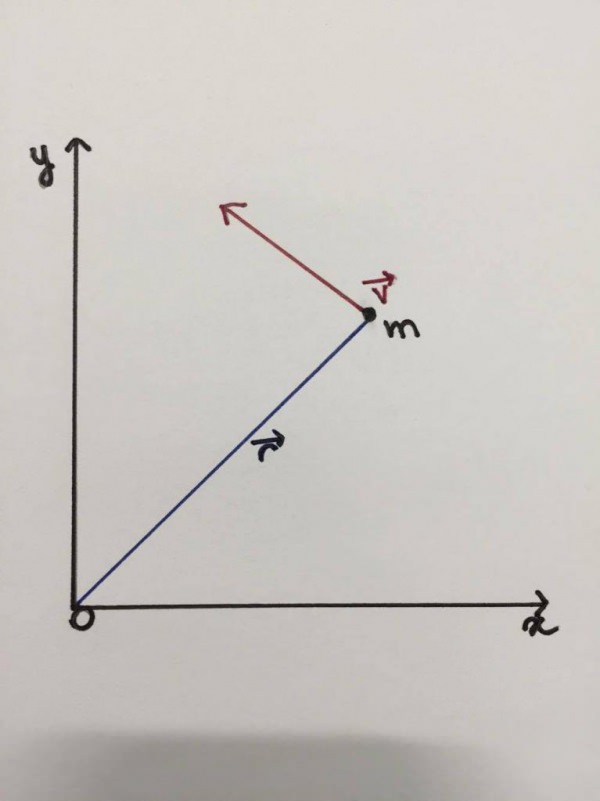
Нижче наведено малюнок, на якому схематично показано, що деяка частка або матеріальна точка масою m робить рух по круговій траєкторії радіусом r зі швидкістю v, спрямованим по дотичній. Вісь обертання розташована перпендикулярно площині рисунка в точці O.

Введемо наступну фізичну величину:

L = r*m*v = r*p.

Вона називається моментом імпульсу, або кутовим моментом. Як видно, це векторна величина. Її напрямок можна визначити за правилом правої руки: необхідно надіслати 4 пальця таким чином, щоб вони, рухаючись вздовж вектора r, приходили до кінця вектора p (або v), тоді великий палець покаже напрям L. В розглянутому випадку L направлений до читача перпендикулярно площині рисунка.

Оскільки на малюнку швидкість (імпульс) частинки спрямована під прямим кутом до вектора r, то наведене рівняння можна переписати у скалярної формі:

L = r*m*v = r*p.

Кутова швидкість і момент інерції

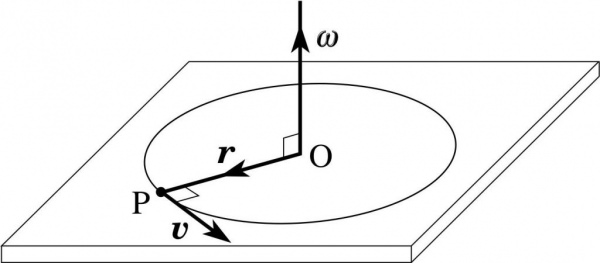
Момент імпульсу частинки з попереднього прикладу можна записати через кутову швидкість ω. Для цього скористаємося її зв’язком зі швидкістю лінійною:

ω = v/r => v = ω*r.

Підставляючи останнє рівність у скалярне рівняння L, отримаємо:

L = r2*m*ω = I*ω, де I = r2*m.

Тут I – це момент інерції частинки. Отриманий вираз використовується часто для вирішення практичних завдань, одна з яких буде розглянуто нижче.

Закон збереження обертального руху

Рух по колу так само, як і лінійне переміщення об’єктів у просторі, характеризується законами збереження. Одним з них є збереження моменту імпульсу. Отримаємо цей закон.

Рівняння розглянутого типу руху має наступний вигляд:

dL/dt = M.

Де dL/dt характеризує зміну моменту імпульсу тіла в часі, коли на нього чинить дію деякий момент M, створюваний зовнішніми (не внутрішніми) силами. Якщо цей момент сил дорівнює нулю, тоді зануляется і ліва частина виразу, що означає L=const. Для цього випадку можна записати таке рівняння:

L = const = I1*ω1 = I2*ω2.

Що означає ця запис? Вона говорить про те, що якщо деяке тіло оберталося зі швидкістю ω1 і мало момент інерції I1, потім унаслідок яких-небудь внутрішніх (не зовнішніх) сил змінився момент інерції і став рівним I2, то нова швидкість обертання ω2 буде пропорційно пов’язана з цією зміною.

Записане співвідношення називається законом збереження моменту імпульсу точки (тіла) за аналогією з відповідним законом для лінійних величин (збереження імпульсу), оскільки роль маси відіграє момент інерції I, а швидкості – кутова величина ω.

Використання закону L = const

Розглянуте в попередньому пункті співвідношення можна бачити у дії, коли виступають фігуристи або балерини. Вони, виконуючи складні акробатичні номери, розкручують своє тіло, розкидаючи при цьому руки і ноги, а потім притискають кінцівки до тіла. Остання дія призводить до зменшення величини I і, відповідно, до збільшення швидкості обертання, що створює досить видовищний ефект.

Іншим прикладом використання незмінності моменту імпульсу системи є реалізація повороту штучного супутника в космічному просторі. Для цього запускають спеціальний прикріплений до нього маховик. Оскільки загальний кутовий момент не повинен змінитися за рахунок дії внутрішніх сил, то сам супутник починає обертатися в протилежному напрямку. Як тільки він повернеться на потрібний кут навколо своєї осі, маховик зупиняють за допомогою електромотора, і корпус супутника також припиняє своє обертання.

Обчислення моменту інерції

Оскільки в законі збереження кругового руху присутній величина I, слід сказати кілька слів про неї. Вона характеризує інерційність системи, тобто наскільки “важко” або “легко” її розкрутити. Наприклад, маховик автомобіля володіє великою масою і відносно великим радіусом, тому його момент інерції є значним. Навпаки, колесо велосипеда зроблено з легкого алюмінієвого обода, тому для нього I буде порівняно невеликим.

Для обчислення цієї фізичної характеристики слід використовувати формулу:

I = ∫m(r2*dm).

Звідки видно, що момент інерції – це характеристика системи, в яку входить тіло обертання, а не самого тіла. Цей факт відрізняє I від лінійної інерції, яка залежить виключно від властивостей тіла (його маси).

Завдання з обертовим стрижнем

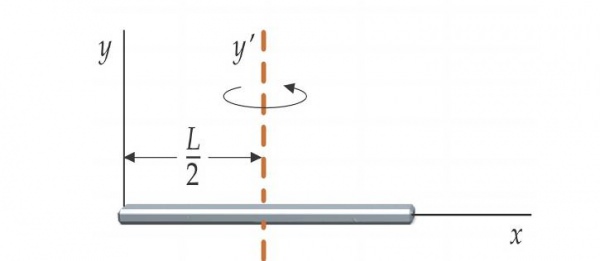
Вирішимо цікаву задачу: є твердий стержень, який обертається навколо осі, розташованої на його кінці. Якщо плавно змістити цю вісь у центр маси стрижня, як зміниться швидкість обертання?

Це класична задача на застосування закону збереження моменту імпульсу. Складність полягає в обчисленні зміни моменту інерції. Для цього можна самостійно скористатися наведеною вище формулою з інтегралом, але простіше буде подивитися необхідні значення I в довідковій літературі.

На початку проходила через вісь обертання кінець стрижня. Для цієї системи момент інерції дорівнює:

I1 = m*L2/3, де L – довжина стрижня, m – його маса.

Коли вісь змістили в центр маси об’єкта, змінився його момент інерції, він став дорівнює:

I2 = m*L2/12.

Застосовуємо закон збереження L, отримуємо:

m*L2/3*ω1 = m*L2/12*ω2 => ω2/ω1 = m*L2/3/(m*L2/12) = 4.

Ми отримали відповідь на завдання: стрижень стане обертатися в 4 рази швидше, ніж спочатку.