Як обчислити площу поверхні циліндра — тема цієї статті. У будь-математичної задачі почати треба з введення даних, визначити, що відомо і чим оперувати надалі, і лише потім приступити безпосередньо до розрахунку.

Дане об’ємне тіло являє собою геометричну фігуру циліндричної форми, обмежену зверху і знизу двома паралельними площинами. Якщо докласти трохи уяви, то можна помітити, що геометричне тіло утворюється обертанням прямокутника навколо осі, причому віссю є одна з його сторін.

Звідси випливає, що описувана крива зверху і знизу циліндра буде окружністю, основним показником якої є радіус або діаметр.

Площа бічної поверхні циліндра

Спочатку потрібно уявити, як виглядає розгортка у двомірному просторі.

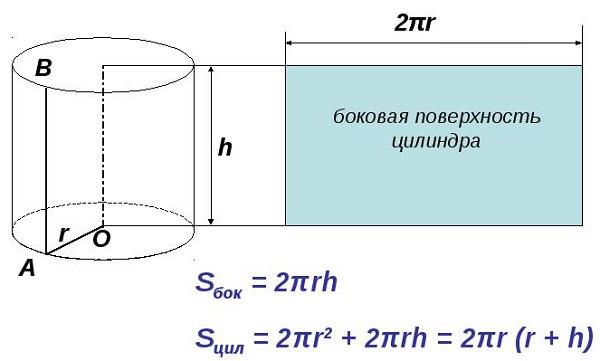
Це не що інше, як прямокутник, одна сторона якого дорівнює довжині кола. Формула її відома з незапам’ятних часів —2π * r, де r — радіус кола. Інша сторона прямокутника дорівнює висоті h. Знайти шукане не складе праці.

S– пліч = 2π * r * h,

де число π = 3.14.