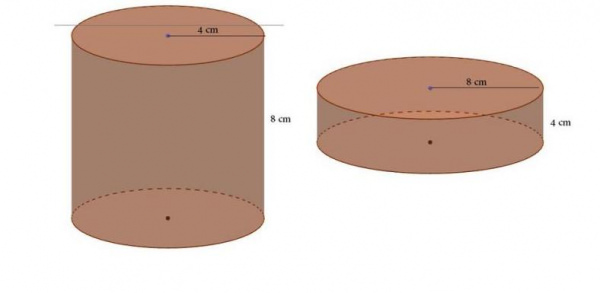
Як відомо, маса в динаміці поступального руху відіграє важливу роль, визначаючи інерційні властивості рухомих тел. У динаміці обертання замість маси користуються моментом інерції. Розглянемо у статті, що це за величина і як визначається момент інерції циліндра відносно осі.

Що таке момент інерції?

Цю величину зазвичай позначають буквою I. Для матеріальної точки математична формула моменту інерції записується так:

I = m*r2.

Де r – відстань до осі обертання від точки масою m. З формули зрозуміло, що одиницею вимірювання величини є кілограми на квадратний метр (кг*м2).

Якщо тіло має складну форму і його об’ємна щільність є змінною, тоді для визначення I слід використовувати таке інтегральне вираження:

I = ∫m(r2*dm) = ∫V(r2*ρ*dV).

Де dm – це елементарна маса, що знаходиться від осі обертання на відстані r.

Таким чином, момент інерції визначає розподіл матерії в тілі складної форми відносно певної осі обертання системи.