Для того, щоб розібратися, як побудувати графік лінійної функції, важливо зрозуміти саму суть функції. Функція — модель залежності зміни одного параметра від іншого.

Тема функціональних залежностей за традицією відкривається лінійною функціональною залежністю. Лінійна — це сама проста залежність. Графік лінійної функції — пряма.

Життя та функції

В житті лінійні залежності зазвичай зустрічаються в ідеальних штучних процесах, зміни в яких приймаються за постійні. Наприклад, коли людина їде кудись з постійною швидкістю.

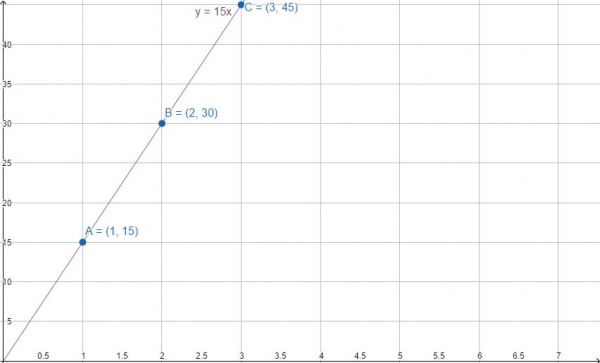
Відстань, яку людина проїде на велосипеді, буде лінійно змінюватися в залежності від кількості годин, які він їде. Якщо 15 кілометрів він проїжджає за годину (точка А), то за дві години він проїде 30 кілометрів (точка В), через три години — 45 (точка С).

Залежність описується рівнянням y = 15x. Як побудувати графік лінійної функції в цьому випадку?

• знайти координати точок, які є рішенням рівняння;
• побудувати їх на координатній площині;
• з’єднати ці точки в лінію.