Для того, щоб розібратися, як побудувати графік лінійної функції, важливо зрозуміти саму суть функції. Функція — модель залежності зміни одного параметра від іншого.
Тема функціональних залежностей за традицією відкривається лінійною функціональною залежністю. Лінійна — це сама проста залежність. Графік лінійної функції — пряма.
Життя та функції
В житті лінійні залежності зазвичай зустрічаються в ідеальних штучних процесах, зміни в яких приймаються за постійні. Наприклад, коли людина їде кудись з постійною швидкістю.
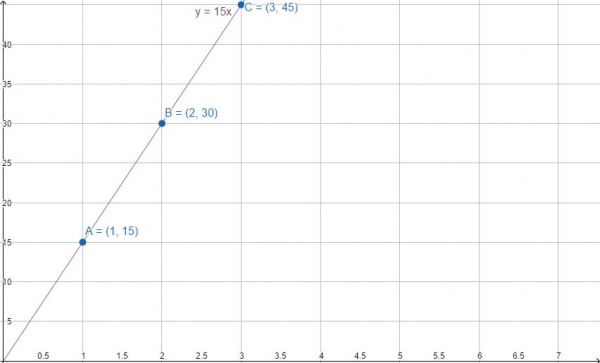
Відстань, яку людина проїде на велосипеді, буде лінійно змінюватися в залежності від кількості годин, які він їде. Якщо 15 кілометрів він проїжджає за годину (точка А), то за дві години він проїде 30 кілометрів (точка В), через три години — 45 (точка С).
Залежність описується рівнянням y = 15x. Як побудувати графік лінійної функції в цьому випадку?
- знайти координати точок, які є рішенням рівняння;
- побудувати їх на координатній площині;
- з’єднати ці точки в лінію.
Опис алгоритму
Пошук координат точок, які є рішенням рівняння зводиться до знаходження двох точок, які однозначно визначають пряму. Хоча досить вибрати два різних значення х і знайти відповідні їм значення y для самоперевірки можна знаходити три пари значень. Це дозволить швидко виявити можливу помилку в обчисленнях. Найчастіше перше значення х вибирають рівним нулю.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| y = 0 | y = 15 |
Друге значення х при великому k краще підбирати поруч з першим. Інакше вийде сильний розкид у значеннях y і x, наприклад, при x = 4 в розглянутому рівнянні y = 60. У кожному разі, до того, як побудувати графік лінійної функції за знайденими значеннями, підбирають масштаб.
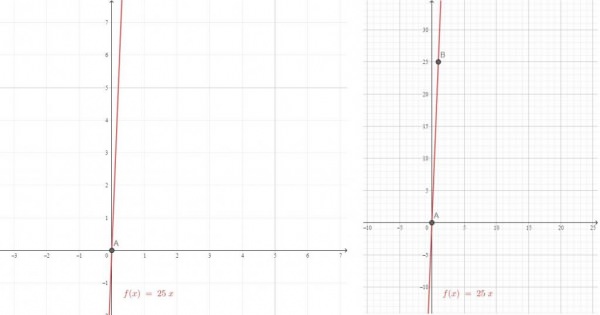
| у = 25 x | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 × 1 | |
| y = 0 | y = 25 |
Коефіцієнт при х
Рівняння лінійної функції має вигляд y = kx + b. В залежності від зміни коефіцієнта при невідомій змінюється і характер графіка лінійної функції y = kx.
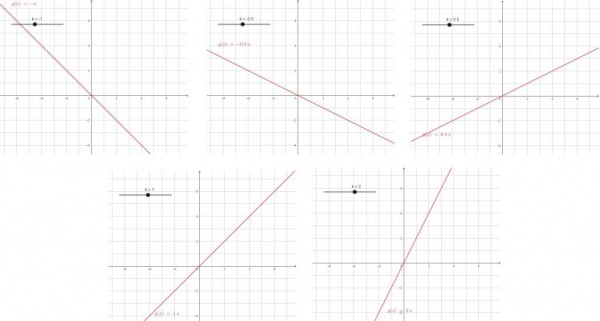
Чим більше по модулю коефіцієнт, тим більшою крутизною має пряма, тим сильніше за одне і те ж зміна значень х змінюються значення y. Коефіцієнт при х виступає коефіцієнтом пропорційності.
Вільний коефіцієнт
Вільний коефіцієнт — стала, яка не залежить від змін значення x. Він показує, де пряма перетинає OY.
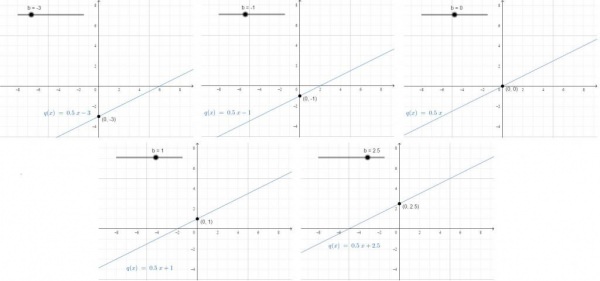
Наприклад, людина з ранку до 12 години дня пройшов 10 кілометрів, а потім три години їхав на велосипеді. Тоді відстань, яку він подолав за день: y = 15 × 3 + 10. Якщо ж ви хочете вивести формулу для підрахунку відстані в кінці кожної години з трьох, які він проїхав на велосипеді, можна скористатися: y = 15x + 10. В годину дня він проїхав 15 × 1 і ще пройшов 10, в дві години він проїхав 15 × 2, але пройшов всі ті ж 10.
Графік лінійної функції y = kx + b описує пряму, яка має кут нахилу k і перетинає OY у точці з координатами (0, b). Аналіз рівняння часто дозволяє вирішувати завдання, не будуючи графік. Але для того, щоб працювати в розумі, дії повинні бути добре закріплені на візуальному матеріалі.
Наприклад, завдання: знайти точки перетину y = – x2 і y = 0,5 x + 5. Перша функція щербатий, друга зростаюча, перша знаходиться нижче другої, т. к. гілки параболи спрямовані вниз, і її вершина знаходиться в початку координат. Лінійна функція повинна була б мати набагато більший кут нахилу, щоб бути більш крутий і перетнути одну з гілок параболи. Тому можна однозначно визначити, що точок перетину ні, не будуючи графік і не виробляючи підстановок.
Приватні випадки
Завдяки аналізу рівняння ще до того, як побудувати графік лінійної функції, можна дізнатися її приблизне розташування на OY і кут нахилу, а значить, і крутизну. Це допомагає не тільки підібрати правильний масштаб і побудувати графік, але й вирішити деякі задачі в розумі.








