Для отримання уявлень про властивості різних фізичних об’єктів і процесів вчені часто вдаються до використання спрощених моделей. Однією з них є модель ідеального газу. Використовуючи її, покажемо, за якою формулою внутрішня енергія газу обчислюється.

Концепція ідеального газу

Під газом ідеальним розуміють такий газ, частинки якого одна з одною не взаємодіють, хаотично рухаються в просторі в різних напрямках, ймовірність їх зіткнення між собою практично дорівнює нулю, відстані між частинками великі в порівнянні з їх лінійними розмірами.

Єдиним процесом, що спостерігається експериментально в макроскопічному масштабі в ідеальній газовій системі, є зіткнення молекул зі стінками посудини. Ці зіткнення вважаються абсолютно пружними, тобто в результаті у них зберігається імпульс частинок і їх кінетична енергія. Розглянутий процес є причиною тиску в газах.

Ідеальним з високим ступенем точності можна вважати будь-газ, який при атмосферних тисках і кімнатних температурах знаходиться в термодинамічній рівновазі. Більш того, система повинна складатися з хімічно нейтральних молекул і атомів, наприклад молекули N2, O2 або благородні гази He, Ar та інші.

Внутрішня енергія ідеального газу

Поняття енергії у фізиці тісно пов’язано з можливістю здійснення роботи. При цьому часто виділяють потенційну енергію, яка міститься в хімічних зв’язках між елементами системи, і кінетичну енергію, пов’язану з поступальним і обертальним переміщенням у просторі цих елементів.

Під внутрішньою енергією розуміють фізичну величину, яка відповідає сумі потенційної і кінетичної енергій системи.

Стосовно до ідеальної газовій системі поняття внутрішньої енергії одержуємо, що вона повинна дорівнювати її кінетичної енергії. Дійсно, так як між молекулами і атомами ідеального газу не існує взаємодій, то потенційна енергія системи буде дорівнює нулю. Таким чином, для ідеального газу завжди справедливо рівність:

U = Ek

Щоб записати формулу внутрішньої енергії ідеального газу, слід обчислити величину Ek для нього.

Визначення кінетичної енергії

Розглянемо закриту систему з ідеальним газом. Припустимо, що кількість частинок в цій системі дорівнює N. Для простоти припустимо, що всі частинки є однаковими. Кожна з них має масу m і рухається з деякою швидкістю v. Вся система знаходиться в термодинамічній рівновазі при абсолютній температурі T. Кінетичну енергію системи можна визначити за такою формулою:

Ek = m / 2 × ∑i=1N (vi2)

Якщо праву частину рівності помножити і поділити на число N, то множник суми буде дорівнює середньої квадратичної швидкості <v>. У такому разі формула кінетичної енергії запишеться так:

Ek = N × m × <v>2 / 2

Тепер згадаємо формулу, яка пов’язує середню кінетичну енергію однієї молекули з температурою системи:

m × <v>2 / 2 = z / 2 × kB × T

Де kB – константа Больцмана, z – число ступенів свободи.

Підставляючи цей вираз у формулу для повної кінетичної енергії Ek, отримаємо рівність:

Ek = z/2 × kB × T × N

Формула внутрішньої енергії газу

Виходячи з формули для Ek, отриманої вище, залишається лише замінити ліву частину рівності на символ U, щоб отримати відповідний вираз для внутрішньої енергії, маємо:

U = z/2 × kB × T × N

Зважаючи великого значення N користуватися цим виразом на практиці вкрай незручно. Тому дане рівність записують в дещо іншій формі, використовуючи поняття універсальної газової константи R і кількості речовини n. Нескладно показати, що справедливо наступне рівність:

n × R = kB × N

Тоді величина U запишеться так:

U= z/2 × n × R × T

Чим вище температура в системі, тим більше її внутрішня енергія.

Тепер скажемо кілька слів про величину z. У разі одноатомного газу вона дорівнює трьом (три поступальних ступеня свободи). Це означає, що U визначиться так:

U1= 3/2 × n × R × T

Якщо молекула газу складається з двох атомів, то z = 5 (до трьох поступальним ступенями свободи додаються ще два обертальні). Внутрішня енергія газу двоатомних розраховується так:

U2= 5/2 × n × R × T

Нарешті, якщо молекули газу є більш складними, то z = 6 (3 поступальних і 3 обертальних ступеня), і формула для U прийме вигляд:

U3= 3 × n × R × T

Приклад розв’язання типової задачі

Вуглекислий газ знаходиться в балоні об’ємом 15 літрів. Балон нагрівають, і його тиск змінюється на величину 0,5 атмосфери. Як змінюється внутрішня енергія газу в результаті нагрівання?

Вирішити задачу можна швидко, якщо згадати рівняння стану ідеального газу. Ось воно:

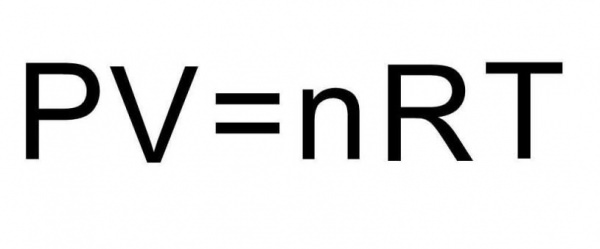
У відповідності з умовою задачі ми вивчаємо ізохорний термодинамічний процес в закритій системі, тобто V=const n=const. В результаті нагрівання в системі змінюється тільки тиск і температура, при цьому залишається справедливою рівність:

ΔP × V = n × R × T

У свою чергу, формула внутрішньої енергії газу CO2 для цього процесу має вигляд:

ΔU3= 3 × n × R × T

Зауважимо, що молекула CO2 є трехатомной, тому для неї z = 6. Порівнюючи два останні рівності, приходимо до кінцевої формулою:

ΔU3= 3 × ΔP × V

Залишається перевести зміна тиску і обсяг з умови задачі в одиниці СІ, підставити їх в отримане рівність і записати відповідь: ΔU3 = +2280 Дж.