Вміння описувати рух по колу є важливим для проведення розрахунків технічних характеристик обертових валів і шестерень. Цей вид руху також зустрічається в побуті і природі, наприклад обертання планет навколо Сонця і фігуристів під час виступу на спортивних змаганнях. У цій статті розглянемо, як з точки зору фізики можна описати цей вид руху.

Динаміка обертання

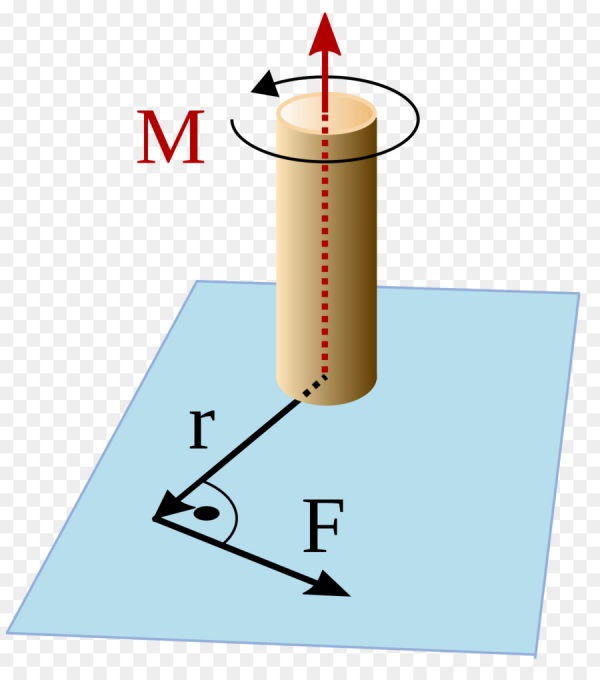
Рух по колу – це обертання деякого тіла або матеріальної точки навколо осі. Щоб тіло почало обертатися, необхідно наявність зовнішнього моменту сил, що діє на розглянуту систему. Цей момент визначається за формулою:

M = F*d

Тут F – сила, d – довжина важеля (відстань між віссю і точкою прикладання сили). Момент сили є величиною векторною. Наведена формула використовується для розрахунку модуля M.

Дія моменту M відбивається на системі у вигляді появи кутового прискорення. Тобто система починає обертатися. Головна формула руху по колу записується у вигляді:

M = I*α

Тут I – момент інерції, α – кутове прискорення. Обидві величини мають свої аналоги для лінійного випадку. Якщо з аналогом величини α все зрозуміло, то для моменту інерції I необхідно пояснити. Величина I відображає інерційні властивості обертової системи. Тобто при обертанні вона грає таку ж роль, як звичайна маса тіла.

Зазначимо, що наведений вираз є аналогом другого закону Ньютона для обертання.